Table of Contents
What Are Adjacent Angles?
Adjacent angles are two angles that share a common arm (side) and a common vertex, yet do not overlap. In other words, they are side by side and share a common side while having different rays extending from that side. The sum of adjacent angles is always equal to the total measure of the angle formed by extending the common side.
In a diagram, if you have a pair of adjacent angles, you can think of them as two angles that are next to each other and share a side. The common side is the one that forms the boundary between the two angles. It’s important to note that for angles to be considered adjacent, they must have both a common side and a common vertex.
For example, in the diagram below, ∠ABC and ∠CBD are adjacent angles because they share the common side BC and the common vertex B.
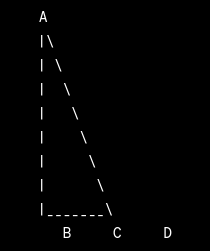
In this case, ∠ABC and ∠CBD are adjacent angles, and their sum (∠ABC + ∠CBD) is equal to the total angle formed by extending the common side BC.
Properties of Adjacent Angles
- Share a common side and vertex.
- Form a linear pair if their non-common sides make a straight line (summing to \(180^\circ\)).
- Have measures that add up to the angle formed by their non-shared sides.
- Can be bisected by the common side.
- Are not necessarily equal in measure.
How to Identify Adjacent Angles
Here’s a step-by-step guide:
- Common Side: Look for two angles that have a side (ray or line segment) in common. This shared side is the one that forms the boundary between the two angles.
- Common Vertex: Check if the two angles also share a common vertex. The vertex is the point where the rays or sides of the angles meet.
- No Overlapping: Ensure that the angles do not overlap. Adjacent angles are side by side, and their interiors do not intersect.
- Linear Pair Test: If the non-common sides of the angles form a straight line, then the angles are a linear pair, which means they are adjacent. The sum of their measures will be \(180^\circ\).
- Verify Properties: Confirm that the angles meet the properties of adjacent angles, such as having a common side and vertex and their measures summing up to the angle formed by their non-shared sides.
For example, in a diagram:
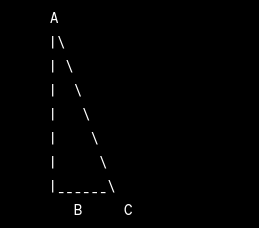
In this illustration, ∠ABC and ∠BCA are adjacent angles because they share the common side BC and the common vertex B.
What Is the Difference between Vertical and Adjacent Angles?
| Vertical Angles | Adjacent Angles |
|---|---|
| Formed by the intersection of two lines. | Formed by having a common side and a common vertex. |
| Always congruent (equal measures). | Not necessarily congruent. |
| Opposite each other when two lines intersect. | Side by side, sharing a common side and vertex. |
| Share a common vertex but no common side. | Share a common side and a common vertex. |
| Example: ∠A and ∠B are vertical angles if lines AB and BC intersect at point B. | Example: ∠ABC and ∠BCD are adjacent angles because they share side BC and vertex B. |