Table of Contents
Definition of Angles
In geometry, an angle is a fundamental geometric concept that describes the inclination or relative orientation of two line segments, rays, or lines that meet at a common point, known as the vertex of the angle. Angles are typically measured in degrees (°) or radians (rad) and are used to quantify the amount of rotation needed to move from one line to another around their common point of intersection.
What Are Angles?
Imagine you have two straight lines, and they meet at a point. This meeting point is called the “vertex.” Now, the space between these lines, where they meet, is called an angle.
We measure angles in degrees. It’s like a way of telling how much the lines are bent at the vertex. A right angle is 90 degrees, and a straight angle is 180 degrees.
So, when you see two lines coming together, you’re looking at an angle. It’s like a little corner or a bend. Angles help us understand how things point or turn, and they’re all around us, from the hands on a clock to the corners of your favorite shape!
Key elements of the definition of angles include:
- Vertex: The vertex is the point where the two lines, rays, or line segments meet. It serves as the center of the angle.
- Sides: The two line segments or rays that form the angle are called its sides. These sides extend from the vertex in different directions.
- Measurement: Angles are measured in degrees, where a full circle consists of 360 degrees, and an angle can be expressed as a specific number of degrees. Alternatively, angles can be measured in radians, with one full rotation equaling 2π radians.
- Orientation: The orientation of the two sides with respect to each other determines the type of angle. Angles can be classified based on their orientation, such as acute (less than 90 degrees), right (exactly 90 degrees), obtuse (greater than 90 degrees but less than 180 degrees), straight (exactly 180 degrees), and more.
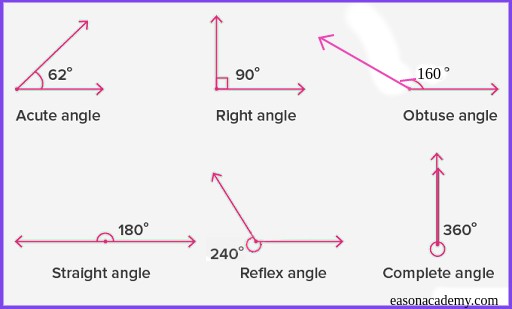
- Acute Angle: An acute angle is smaller than 90 degrees at the vertex. It’s like a little angle, less than a right angle.
Types of Angles
- Obtuse Angle: An obtuse angle falls between 90 and 180 degrees. It’s wider than a right angle, like a stretched-out angle.
- Right Angle: A right angle is exactly 90 degrees at the vertex, forming an “L” shape.
- Straight Angle: A straight angle measures precisely 180 degrees, like a straight line.
- Reflex Angle: A reflex angle is between 180 and 360 degrees. It’s wider than a straight angle, like an open angle.
- Complete Angle: A complete angle, which equals 360 degrees, is like going in a full circle. It’s like turning all the way around.
Properties and Characteristics of Angles
Angles possess various properties and characteristics that help us understand and work with them in geometry. Here are some of the fundamental properties and features of angles:
- Vertex: Every angle has a vertex, which is the common endpoint where two rays or line segments meet. The vertex is like the center of the angle.
- Sides: Angles have two sides that extend from the vertex. These sides determine the angle’s measurement and classification.
- Measurement: The measurement of an angle is typically expres sed in degrees (°) or radians (rad). The degree measure indicates the amount of rotation required to move from one side to the other around the vertex.
- Orientation: The relative orientation of the two sides of an angle is what gives it its specific type or classification, such as acute, obtuse, right, straight, or reflex.
- Interior: The space inside the angle, between its sides, is called the interior of the angle. The interior is where we find the actual angle measurement.
-
Exterior: The region outside the angle, surrounding its sides, is referred to as the exterior. It’s the space beyond the angle.
- Angle Sum: When two angles share a common vertex and their sides form a straight line, the sum of the two angles is always 180 degrees. This property is known as the interior angle sum of a straight line.
- Vertical Angles: When two lines intersect, they create pairs of opposite or vertical angles. Vertical angles are always congruent, which means they have the same measurement.
- Adjacent Angles: Adjacent angles are angles that share a common side and a common vertex but do not overlap. They are often found in geometric figures, especially polygons.
- Corresponding Angles: When a pair of parallel lines is intersected by a transversal, corresponding angles are formed. Corresponding angles have the same measurement and are in similar positions relative to the parallel lines.
-
Alternate Interior and Exterior Angles: These angles are formed when a transversal intersects two parallel lines. Alternate interior angles are congruent, and alternate exterior angles are also congruent.
- Complementary Angles: Two angles are complementary if their sum is 90 degrees. For example, an angle measuring 30 degrees and an angle measuring 60 degrees are complementary.
- Supplementary Angles: Two angles are supplementary if their sum is 180 degrees. An angle measuring 120 degrees and an angle measuring 60 degrees are supplementary.
- Bisector: An angle bisector is a line or ray that divides an angle into two equal parts, creating two congruent angles.
Solved Examples On Angles
Example 1: Find the complement of an angle that measures 25 degrees.
Solution: The complement of an angle is the angle that, when added to the given angle, equals 90 degrees. So, to find the complement, subtract the given angle from 90 degrees:
Complement = 90° – 25° = 65°
The complement of an angle measuring 25 degrees is 65 degrees.
Example 2: If two angles are supplementary, and one of them measures 120 degrees, what is the measurement of the other angle?
Solution: Supplementary angles add up to 180 degrees. So, to find the measurement of the other angle, subtract 120 degrees from 180 degrees:
Other angle = 180° – 120° = 60°
The other angle measures 60 degrees.
Example 3: In a quadrilateral, three interior angles measure 80 degrees, 100 degrees, and 120 degrees. What is the measurement of the fourth interior angle?
Solution: The sum of the interior angles in a quadrilateral is always 360 degrees. To find the fourth angle, subtract the sum of the given angles from 360 degrees:
Fourth angle = 360° – (80° + 100° + 120°) = 360° – 300° = 60°
The fourth interior angle measures 60 degrees.
Example 4: In a triangle, one interior angle measures 50 degrees, and the second interior angle measures 70 degrees. What is the measurement of the third interior angle?
Solution: The sum of the interior angles in a triangle is always 180 degrees. To find the third angle, subtract the sum of the given angles from 180 degrees:
Third angle = 180° – (50° + 70°) = 180° – 120° = 60°
The third interior angle measures 60 degrees.
FAQs
Q1: What is an angle in geometry?
A1: An angle in geometry is the figure formed by two rays or line segments with a common endpoint, known as the vertex. It measures the inclination or orientation between these rays and is typically measured in degrees or radians.
Q2: What are the different types of angles?
A2: There are several types of angles, including acute angles (less than 90 degrees), right angles (exactly 90 degrees), obtuse angles (greater than 90 degrees but less than 180 degrees), straight angles (exactly 180 degrees), and reflex angles (greater than 180 degrees).
Q3: How do I find the complement of an angle?
A3: To find the complement of an angle, subtract its measurement from 90 degrees. The complement of an angle plus the original angle will always equal 90 degrees.
Q4: What are supplementary angles?
A4: Supplementary angles are two angles whose sum is 180 degrees. In other words, when you add the measurements of supplementary angles, the result is always 180 degrees.
Q5: What are interior angles in a polygon?
A5: Interior angles in a polygon are the angles formed inside the shape when you connect the vertices of the polygon. The sum of the interior angles in a polygon depends on the number of sides and can be calculated using the formula (n – 2) * 180 degrees, where ‘n’ is the number of sides.
Q6: What are exterior angles in a polygon?
A6: Exterior angles in a polygon are the angles formed outside the shape when you extend one side of the polygon. The exterior angle at a vertex is supplementary to the interior angle at the same vertex.
Q7: How are angles used in everyday life?
A7: Angles have practical applications in various fields, such as construction, architecture, navigation, art, and engineering. They are used for measuring and calculating directions, designing structures, and creating aesthetically pleasing compositions.
Q8: What is the sum of the angles in a triangle?
A8: The sum of the angles in a triangle is always 180 degrees. This property is a fundamental concept in geometry and helps in solving problems related to triangles.