Polygons are fundamental geometric shapes in math that consist of straight-line segments connected end-to-end to form a closed figure. Polygons are an integral part of geometric analysis and understanding, playing a pivotal role in mathematics, architecture, design, and various real-world scenarios. Their properties, such as the sum of interior angles, are key components in geometry, making polygons a fundamental concept in the study of shapes and structures.
Table of Contents
What are Polygons?
The term “polygon” is derived from the Greek words “poly,” meaning “many,” and “gonia,” meaning “angle.” This etymology reflects the fact that polygons are made up of numerous angles where sides meet. A polygon is a two-dimensional closed shape with three or more straight sides. It is created by connecting line segments, called sides, to form a closed path.
These sides intersect at points called vertices (singular: vertex) to create a closed path. Polygons can have three or more sides, and they are a crucial element of geometry. Here are some key characteristics of polygons:
- Straight Sides: The sides of a polygon are straight-line segments, meaning they do not curve.
- Closed Shape: A polygon is a closed figure, which means the sides connect to form a closed path, enclosing an interior space.
- Vertices: Polygons have vertices, which are the points where the sides meet. The number of vertices in a polygon is equal to the number of sides.
- Interior and Exterior: The interior of a polygon is the space enclosed by its sides, while the exterior is the area outside the polygon.
- Variety of Shapes: Polygons come in a wide variety of shapes and sizes. Some have equal side lengths and angles, making them regular polygons, while others have varying side lengths and angles, making them irregular polygons.
- Convex and Concave: Polygons can be classified as convex or concave. Convex polygons have all interior angles less than 180 degrees, while concave polygons have at least one interior angle greater than 180 degrees.
- Sum of Interior Angles: The sum of the interior angles in any polygon can be calculated using the formula: (n−2)×180 degrees, where n is the number of sides.
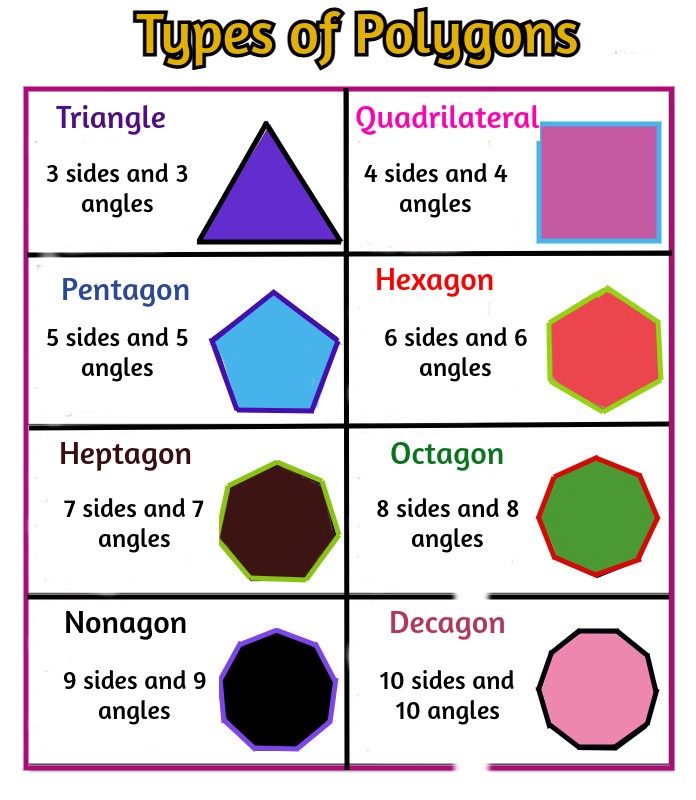
Types of Polygons
Polygons, two-dimensional closed shapes formed by connecting straight-line segments, come in a variety of types based on their properties and characteristics. Here are some common types of polygons:
- Triangle: A triangle is a polygon with three sides and three angles. It is the simplest polygon and can be classified further based on the measures of its angles and the lengths of its sides.
- Quadrilateral: A quadrilateral is a polygon with four sides and four angles. It includes shapes like squares, rectangles, parallelograms, rhombi, and trapezoids.
- Pentagon: A pentagon has five sides and five angles. It can be regular (all sides and angles equal) or irregular (sides and angles of varying lengths and measures).
- Hexagon: A hexagon consists of six sides and six angles. Like other polygons, it can be regular or irregular.
- Heptagon: A heptagon is a seven-sided polygon, and it can also be regular or irregular.
- Octagon: An octagon features eight sides and eight angles. Octagons are commonly used in various applications, including stop signs.
- Nonagon: A nonagon has nine sides and nine angles. Like other polygons, it can be regular or irregular.
- Decagon: A decagon has ten sides and ten angles. It can be classified into regular and irregular types based on its properties.
- Dodecagon: A dodecagon consists of twelve sides and twelve angles. It is less common but follows the same principles as other polygons.
-
Regular Polygon: Regular polygons have equal side lengths and equal interior angles, making them symmetrical. Examples include regular triangles, squares, pentagons, and hexagons.
- Irregular Polygon: Irregular polygons do not have all sides and angles of equal length or measure. They exhibit variation in side lengths and angles.
- Convex Polygon: Convex polygons have all interior angles less than 180 degrees, meaning they do not “cave in.” They are often used in geometry and design.
- Concave Polygon: Concave polygons have at least one interior angle greater than 180 degrees. They have “caved-in” regions, making them more complex to work with.
Polygon Chart
| Polygon | Number of Sides | Regular/ Irregular | Convex/ Concave |
|---|---|---|---|
| Triangle | 3 | Regular | Convex |
| Quadrilateral | 4 | Regular/ Irregular | Convex/ Concave |
| Pentagon | 5 | Regular/ Irregular | Convex/ Concave |
| Hexagon | 6 | Regular/ Irregular | Convex/ Concave |
| Heptagon | 7 | Regular/ Irregular | Convex/ Concave |
| Octagon | 8 | Regular/ Irregular | Convex/ Concave |
| Nonagon | 9 | Regular/ Irregular | Convex/ Concave |
| Decagon | 10 | Regular/ Irregular | Convex/ Concave |
| Dodecagon | 12 | Regular/ Irregular | Convex/ Concave |
Difference Between Regular and Irregular Polygons
| Characteristic | Regular Polygons | Irregular Polygons |
|---|---|---|
| Side Lengths | All sides are equal in length. | Sides have varying lengths. |
| Angle Measures | All angles are equal in measure. | Angles have varying measures. |
| Symmetry | Symmetrical in shape and structure. | Asymmetrical in shape and structure. |
| Vertex Arrangement | Vertices are evenly distributed. | Vertices can be irregularly placed. |
| Properties | Specific formulas for area and perimeter. | Formulas can differ for each irregular shape. |
| Examples | Equilateral triangle, square, regular hexagon. | Scalene triangle, rectangle, irregular pentagon. |
Regular Polygons and Irregular Polygons
Regular polygons are geometric shapes where all sides have the same length, and all interior angles are equal. They exhibit a high degree of symmetry, making calculations and design work more predictable and manageable. Common examples include equilateral triangles, squares, and hexagons, often found in architecture and engineering for their symmetry and aesthetic appeal. In contrast, irregular polygons lack such uniformity, with sides and angles of varying lengths and measures. These shapes are encountered in non-standard geometric figures and unique designs, making them more complex for calculations and adding diversity to artistic and real-world applications. Understanding the distinctions between regular and irregular polygons is essential for both the precision of mathematical analysis and the creativity of design.
Polygon Formulas
Here are some key formulas and equations related to polygons:
- Perimeter of polygons
- Area of polygons
The perimeter of a polygon is the total length of its sides. The formula for finding the perimeter of a polygon depends on whether it’s a regular polygon (all sides are equal in length) or an irregular polygon (sides have varying lengths).
For Regular Polygons:
If you have a regular polygon with nn sides, and each side has a length ss, the perimeter (P) can be calculated as:
P= n⋅s
Simply multiply the number of sides (nn) by the length of one side (ss) to find the perimeter.
For Irregular Polygons:
In the case of an irregular polygon, where the sides have different lengths, you can find the perimeter by adding the lengths of all the sides. If you have the lengths of the individual sides (e.g., s1, s2, s3…), the perimeter (P) is:
P = s1 + s2 + s3 + …
Sum up the lengths of all the sides to determine the perimeter of the irregular polygon.
Area of polygons
The area of a polygon is the measure of the space enclosed by its sides. The formula for calculating the area of a polygon depends on the type of polygon and the information you have.
For Irregular Polygons:
For irregular polygons, the area can be calculated by breaking the shape into smaller, more manageable parts, such as triangles and trapezoids, finding the area of each part, and then summing those areas to get the total area of the polygon.
These are some common methods for finding the area of polygons. The specific method to use depends on the type of polygon and the information available about the shape.
FAQs
What is a polygon?
A polygon is a two-dimensional closed shape formed by connecting straight-line segments. It has sides, vertices (corners), and interior angles.
How many sides does a polygon have?
A polygon can have as few as three sides or many more. It is defined as any closed shape formed by at least three straight-line segments.
What is the sum of interior angles in a polygon?
The sum of the interior angles of a polygon can be calculated using the formula (n−2)×180 degrees, where nn is the number of sides.
What is the exterior angle of a polygon?
The exterior angle of a polygon is the supplement of its corresponding interior angle, meaning 180 degrees minus the interior angle.
What is the difference between regular and irregular polygons?
Regular polygons have all sides and angles equal, while irregular polygons have sides and angles of varying lengths and measures.
What is the perimeter of a polygon?
The perimeter of a polygon is the total length of its sides. For regular polygons, you can use the formula P=n × side length, while for irregular polygons, you add the lengths of all sides.
Can polygons be concave?
Yes, polygons can be concave, meaning they have at least one interior angle greater than 180 degrees. Convex polygons have all interior angles less than 180 degrees.