Amortization

What Is Amortization?

Amortization is a financial term referring to the gradual reduction of a debt or an intangible asset over a specific period. In the context of loans or debt, it involves the systematic repayment of the principal amount along with the interest over time. For intangible assets, such as patents or trademarks, amortization represents the process of allocating the asset’s cost over its estimated useful life.

Key Points:

1. Loan Amortization:

   • In loan amortization, periodic payments consist of both principal and interest.
   • Initially, a larger portion of the payment goes toward interest, while the principal repayment gradually increases over the loan term.
   • Amortization schedules outline the breakdown of each payment, showing how much goes towards interest and how much towards reducing the principal.

2. Intangible Asset Amortization:

   • Companies amortize intangible assets to spread their cost over the asset’s useful life.
   • The amortization expense is recorded on the income statement, reflecting the portion of the asset’s cost expiring during the period.

3. Straight-Line Amortization:

   • One common method is straight-line amortization, where the same amount is amortized each period.
   • For loans, this ensures consistent payments, while for intangible assets, it evenly allocates the cost over the asset’s life.

4. Reducing Balance Amortization:

   • Another method is reducing balance amortization, where the amortization amount decreases over time.
   • This method is common in mortgage loans, where interest is calculated on the remaining balance.

5. Amortization Period:

   • The length of the amortization period depends on the terms of the loan or the estimated useful life of the intangible asset.
   • Shorter periods typically result in higher periodic payments but lower overall interest payments.

6. Tax Implications:

   • Amortization expenses for intangible assets may have tax implications, potentially affecting the company’s taxable income.

Amortization of Loans

Amortization of loans is the gradual repayment of a loan over time through a series of periodic payments. Each payment covers both the principal amount borrowed and the interest accrued. In the initial stages, a larger portion of the payment goes toward interest, while the remainder is applied to reduce the loan principal. Over the course of the loan term, the proportion allocated to principal increases. This systematic approach ensures that the entire loan amount is paid off by the end of the agreed-upon period. Amortization schedules detail the breakdown of each payment, helping borrowers understand how their money is distributed between interest and reducing the outstanding loan balance.

How to calculate loan amortization

Calculating loan amortization involves determining the periodic payments required to fully repay a loan over its term. The most common method is to use the formula for an amortizing loan, which considers the principal amount, interest rate, and loan term. Here are the steps to calculate loan amortization:

Formula for Loan Amortization:

\[ P = \frac{r \cdot PV}{1 – (1 + r)^{-n}} \]

Where:

• P is the periodic payment.
• r is the periodic interest rate (annual interest rate divided by the number of compounding periods per year).
• PV is the present value or principal amount of the loan.
• n is the total number of payments or compounding periods.

Step-by-Step Calculation:

1. Determine Periodic Interest Rate (r):

Convert the annual interest rate to a periodic rate by dividing it by the number of compounding periods per year. For example, if the loan compounds monthly, divide the annual rate by 12.

r = \(\frac{\text{annual interest rate}}{\text{number of compounding periods per year}}\)

2. Identify Loan Parameters:

Know the principal amount of the loan (PV), the periodic interest rate (r), and the total number of payments or compounding periods (n).

• \(PV = \text{principal amount of the loan}\)
• \(r = \text{periodic interest rate}\)
• \(n = \text{total number of payments or compounding periods}\)

3. Use the Formula:

Plug these values into the loan amortization formula to calculate the periodic payment (P).

\[ P = \frac{r \cdot PV}{1 – (1 + r)^{-n}} \]

4. Example Calculation:

Suppose you have a $10,000 loan with an annual interest rate of 5%, compounded monthly over 3 years (36 months).

• r = \(  \frac{0.05}{12} \quad (\text{monthly interest rate}) \)
• n = \( 36 \quad (\text{number of monthly payments}) \)
• PV = \( $10,000 \quad (\text{principal amount}) \)

5. Calculate P:

Use a calculator or spreadsheet to find the value of P.

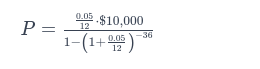
6. Review Amortization Schedule:

Create an amortization schedule that outlines each payment, the portion going to interest, the portion to principal, and the remaining balance.

Pros and Cons of Loan Amortization

Pros:

1. Structured Repayment: Loan amortization provides a structured repayment plan, allowing borrowers to systematically reduce their debt over time. Each installment contributes to both principal and interest, ensuring a gradual reduction in the outstanding balance.
2. Predictable Payments: Borrowers benefit from predictability in payments. Fixed periodic payments simplify budgeting and financial planning, making it easier for individuals and businesses to manage their cash flow.
3. Interest Reduction: Over the course of the loan, a larger portion of each payment goes toward principal repayment. This results in a reduction of interest costs over time, helping borrowers save on the total cost of the loan.
4. Clear Schedule: Amortization schedules provide a clear roadmap of payments, detailing how much goes toward interest and principal for each installment. This transparency helps borrowers understand the progression of their loan.

Cons:

1. Higher Initial Interest Payments: In the early stages of loan amortization, a larger portion of the payment goes toward interest. This means that borrowers may pay a significant amount of interest before making a substantial impact on the principal.
2. Rigidity in Payments: While predictable payments are an advantage, they can be a disadvantage if financial circumstances change. Borrowers may find it challenging to adjust payments during periods of financial strain, potentially leading to financial stress.
3. Potential for Negative Equity: In certain situations, such as with long-term mortgages, borrowers may experience negative equity, where the outstanding loan amount exceeds the value of the asset. This can be a concern if property values decline.
4. Prepayment Penalties: Some loans may have prepayment penalties, discouraging borrowers from paying off the loan early. This can limit the flexibility of borrowers who wish to accelerate their repayment schedule.

Why Is Amortization Important?

Amortization is important for several reasons. It provides a structured and systematic way to repay loans, making it easier for borrowers to manage their finances. The process ensures that each payment contributes to both principal and interest, gradually reducing the outstanding debt over time. This predictability allows for better financial planning and budgeting, making it clear to borrowers how much they owe and when they will fully repay their loans. Amortization is also crucial for lenders as it helps them assess risk and allocate interest income appropriately. Overall, amortization plays a key role in financial transparency, reducing the total cost of borrowing, and facilitating responsible debt management.

Amortization vs. Depreciation

Amortization and depreciation are methods businesses use to handle the costs of different types of things they own. Amortization is for things you can’t touch, like patents or software, helping to show how their value decreases over time. Depreciation is for physical items, like machines or buildings, spreading out their costs as they wear out. The key difference is that amortization deals with intangible things, while depreciation deals with physical items. Both methods help businesses manage their finances by showing how the value of their assets changes over the years.