Diameter of a Circle – Definition, Examples

In the world of geometry, circles are among the most captivating and fundamental shapes, known for their symmetry and ubiquity. One of the key elements that defines a circle is its diameter. In this article, we will explore the concept of the diameter of a circle, understand its significance, and examine how it is used in various applications.

What is the Diameter of a Circle?

Diameter, in the context of a circle, is a crucial geometric property. It is defined as a straight line segment that passes through the center of the circle and connects two points on the circle’s circumference. Essentially, the diameter is the widest possible distance within a circle.

Diameter Symbol

The symbol for diameter, often used in technical drawings and mathematics, looks like a tiny circle with a line running across it. It’s represented as “⌀”. This symbol is a simple and clear way to show the size or width of a circle or cylindrical object.

Formulas for the Diameter of a Circle

The formula for the diameter of a circle is straightforward and can be expressed in terms of the radius or circumference of the circle. Here are the primary formulas for calculating the diameter:

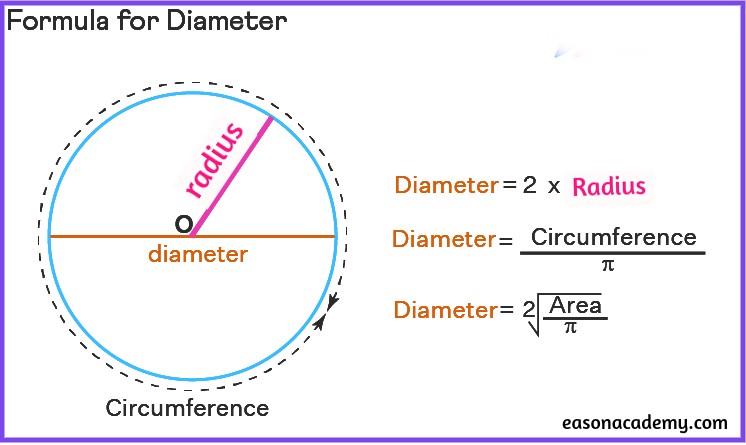
1.Diameter Formula Using the Radius:

The diameter is related to another essential measurement of a circle: the radius. The radius (denoted as “r”) is the distance from the center of the circle to its edge. The relationship between the diameter and the radius is straightforward:

Diameter (d) = 2 * Radius (r)

In this formula, “d” represents the diameter, and “r” represents the radius. Therefore, the diameter is always twice the length of the radius.

2. Diameter Formula Using the Circumference:

• The diameter is related to the circumference (C) through the mathematical constant π (pi).
• Formula: d = C / π

3. Diameter Formula Using Area of Circle

The diameter of a circle is not directly calculated from the area of the circle. However, you can find the diameter of a circle if you know its area by using the formula for the area and the formula for the radius.

The formula for the area of a circle is:
A = πr²

If you know the area (A) and want to find the diameter (d), you can follow these steps:

1. Solve for the radius (r) in terms of the area (A):
   r = √(A / π)
2. Once you have the radius, you can find the diameter using the formula:
   d = 2r

So, the formula for finding the diameter of a circle using its area is:
d = 2√(A / π)

This formula allows you to determine the diameter when you know the area of the circle.

Diameter Properties

Here are the properties of the diameter of a circle explained in simple points:

1. Length: The diameter is the longest line you can draw inside a circle, from one side to the other.
2. Center: It passes through the center of the circle.
3. Twice the Radius: The diameter is always two times longer than the radius, which is the distance from the center to the edge of the circle.
4. Maximum Distance: It represents the longest distance between any two points on the circle’s edge.
5. Circumference: The circumference (the distance around the circle) is equal to π times the diameter.
6. Symmetry: It acts as a line of symmetry, meaning the circle looks the same on both sides when folded along the diameter.
7. Geometry: It’s used as a reference to create other shapes and geometric constructions.
8. Practical Use: The diameter is important in real-world applications like designing wheels, roads, and structures for stability and measurements.

Solved Examples

Example 1: Suppose you have a circular swimming pool with an area of 100 square meters. Calculate the diameter of the pool.

Solution:

1. First, find the radius using the formula for the area of a circle:
   A = πrr²
   100 m² = πr²
2. Solve for the radius (r):
   r² = 100 m² / π
   r ≈ √(100 m^2 / π) ≈ √(31.83) ≈ 5.65 meters
3. Finally, find the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 5.65 meters ≈ 11.30 meters

So, the diameter of the circular swimming pool is approximately 11.30 meters.

Example 2: Imagine you have a circular garden with an area of 400 square feet. Calculate the diameter of the garden.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   400 ft² = πr²
2. Solve for the radius (r):
   r² = 400 ft² / π
   r ≈ √(400 ft² / π) ≈ √(127.28) ≈ 11.28 feet
3. Determine the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 11.28 feet ≈ 22.56 feet

The diameter of the circular garden is approximately 22.56 feet.

Example 3: Suppose there’s a circular pond with an area of 314 square meters. Find the diameter of the pond.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   314 m² = πr²
2. Solve for the radius (r):
   r² = 314 m² / π
   r ≈ √(314 m² / π) ≈ √(100) ≈ 10 meters
3. Calculate the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 10 meters = 20 meters

The diameter of the circular pond is 20 meters.

Example 4: Suppose you have a circular garden with an area of 200 square yards. Calculate the diameter of the garden.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   200 yd² = πr²
2. Solve for the radius (r):
   r² = 200 yd² / π
   r ≈ √(200 yd² / π) ≈ √(63.66) ≈ 7.98 yards
3. Determine the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 7.98 yards ≈ 15.96 yards

The diameter of the circular garden is approximately 15.96 yards.

Example 5: You have a circular tabletop with an area of 500 square inches. Find the diameter of the tabletop.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   500 in² = πr²
2. Solve for the radius (r):
   r²= 500 in² / π
   r ≈ √(500 in² / π) ≈ √(159.15) ≈ 12.63 inches
3. Calculate the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 12.63 inches ≈ 25.26 inches

The diameter of the circular tabletop is approximately 25.26 inches.

Example 6: Suppose there’s a circular park with an area of 1,256 square meters. Calculate the diameter of the park.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   1,256 m² = πr²
2. Solve for the radius (r):
   r² = 1,256 m²/ π
   r ≈ √(1,256 m² / π) ≈ √(400) ≈ 20 meters
3. Determine the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 20 meters = 40 meters

The diameter of the circular park is 40 meters.

Example 7:Imagine you have a circular window with an area of 1,000 square inches. Calculate the diameter of the window.

Solution:

1. Find the radius using the formula for the area of a circle:
   A = πr²
   1,000 in² = πr²
2. Solve for the radius (r):
   r² = 1,000 in² / π
   r ≈ √(1,000 in² / π) ≈ √(318.31) ≈ 17.85 inches
3. Calculate the diameter (d) using the formula for the diameter:
   d = 2r
   d = 2 * 17.85 inches ≈ 35.70 inches

The diameter of the circular window is approximately 35.70 inches.