Today, we’re diving into the fantastic world of circles and learning about something super cool: the radius! But what is it, and why is it important? Let’s find out.
Table of Contents
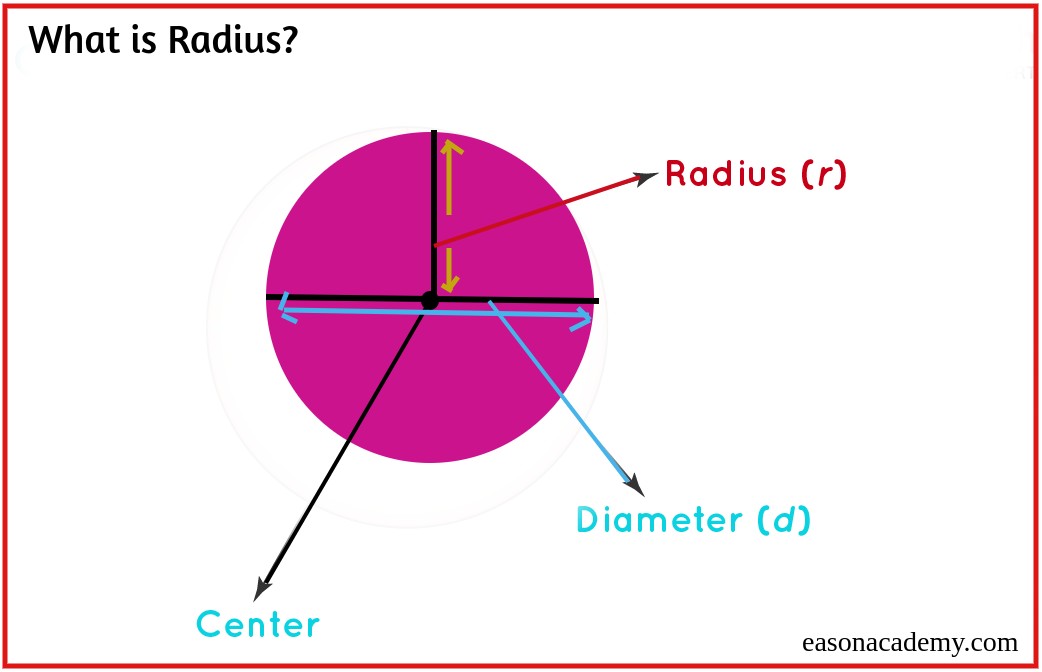
What’s the Radius?
The radius of a circle is the distance from its center to the edge. Think of it as the circle’s “halo.”
Why Is the Radius Matters
1. Area: To find the area of a circle, use the formula A = π * r2,
where “r” is the radius.
This helps you measure the space inside the circle.
2. Circumference: For the distance around a circle (circumference), use the formula C = 2 * π * r. It’s like measuring the circle’s waistline.
In Circle Geometry
- The diameter is just twice the radius.
- Chords (line segments connecting two points on the circle) often involve the radius.
Radius Formula with Diameter
You can express the radius of a circle in terms of its diameter using a simple formula:
Radius (r) = Diameter (d) / 2
In this formula:
- r represents the radius of the circle.
- d represents the diameter of the circle.
To find the radius when you know the diameter, you simply divide the diameter by 2.
Radius Formula using Area
You can find the radius of a circle using its area if you know the area. The formula to find the radius (r) from the area (A) of a circle is as follows:
Radius (r) = √(A / π)
In this formula:
- r represents the radius of the circle.
- A represents the area of the circle.
- π (pi) is a mathematical constant approximately equal to 3.14159.
To find the radius when you know the area, you take the square root of the area divided by π. This formula is derived from the formula for the area of a circle:
Area (A) = πr2
If you know the area (A) and want to find the radius (r), you rearrange the formula as follows:
r = √(A / π)
How to Find the Radius of a Circle?
You can find the radius of a circle using different methods, depending on the information you have about the circle. Here are several methods to find the radius of a circle:
-
Given Diameter:
- If you have the diameter of the circle (d), you can find the radius using the formula: Radius (r) = Diameter (d) / 2
- This is the simplest and most direct method. It involves dividing the diameter by 2 because the radius is half of the diameter.
-
Given Circumference:
- If you know the circumference (C) of the circle and you want to find the radius, you can use the formula: Radius (r) = C / (2π)
- In this formula, you divide the circumference by 2π, as the circumference is equal to 2π times the radius.
-
Given Area:
- If you know the area (A) of the circle, you can find the radius using the formula: Radius (r) = √(A / π)
- Here, you take the square root of the area divided by π.
Radius of Circle Examples
Here are a few examples of how to find the radius of a circle using different methods:
Example 1: Given Diameter
Suppose you have a circle with a diameter of 10 centimeters, and you want to find the radius:
Radius (r) = Diameter (d) / 2
(r) = 10 cm / 2
Radius (r) = 5 cm
So, the radius of the circle is 5 centimeters.
Example 2: Given Circumference
Let’s say you know the circumference of a circle is 31.42 centimeters, and you want to find the radius:
Radius (r) = Circumference (C) / (2π)
(r) = 31.42 cm / (2 * 3.14159)
Radius (r) ≈ 5 cm
The radius of the circle is approximately 5 centimeters.
Example 3: Given Area
Suppose you have the area of a circle, which is 25 square inches, and you want to find the radius:
Radius (r) = √(Area (A) / π)
Radius (r) = √(25 in² / 3.14159)
(r) ≈ √(7.96)
Radius (r) ≈ 2.82 in
The radius of the circle is approximately 2.82 inches.
Example 4: You have a circle with a chord (a straight line segment that connects two points on the circle) that is 8 inches long, and the central angle formed by this chord is 60 degrees. You want to find the radius.
You can use trigonometry to find the radius. The radius (r) is related to the chord (c) and the central angle (θ) as follows:
Radius (r) = (c / 2) / sin(θ / 2)
(r) = (8 inches / 2) / sin(60° / 2)
Radius (r) = 4 inches / sin(30°)
(r) = 4 inches / 0.5
Radius (r) = 8 inches
So, the radius of the circle is 8 inches.
FAQs on Radius of Circle
1. What is the radius of a circle?
Answer: The radius of a circle is the distance from the center of the circle to any point on the circle’s edge. It is denoted by “r.”
2. How do I find the radius of a circle if I know the diameter?
Answer: To find the radius from the diameter, you can use the formula: Radius (r) = Diameter (d) / 2.
3. Can I find the radius of a circle if I know its circumference?
Answer: Yes, you can find the radius if you know the circumference using the formula: Radius (r) = Circumference (C) / (2π).
4. Is there a way to calculate the radius if I have the area of the circle?
Answer: Yes, you can find the radius from the area using the formula: Radius (r) = √(Area (A) / π).
5. What are the units for the radius of a circle?
Answer: The units for the radius can be any length unit (e.g., inches, centimeters, meters) depending on the measurement system you are using.
6. How do I find the radius of a circle if I have a point on its circumference and the center?
Answer: The radius is simply the distance from the center to any point on the circle. Measure the distance between the center and the point on the circumference to find the radius.
7. Can I use trigonometry to find the radius of a circle if I have information about a chord and a central angle?
Answer: Yes, you can use trigonometry. The formula is: Radius (r) = (Chord (c) / 2) / sin(θ / 2), where “c” is the chord’s length, and “θ” is the central angle.
8. What is the geometric construction method to find the radius of a circle?
Answer: You can use a compass and straightedge to draw a circle and then construct the radius. Draw two radii from the center to the circle’s edge, and the length of either radius will be the circle’s radius.
9. Are there any special cases where finding the radius of a circle is different from the standard methods?
Answer: In standard geometry, the methods mentioned cover most cases. However, in advanced mathematics or specialized applications, there can be unique cases that require specific approaches.
10. How is the radius related to the diameter and circumference of a circle?
Answer: The radius is half the length of the diameter, and the circumference of a circle is equal to 2π times the radius (C = 2πr).