A heptagon, as the name suggests, is a polygon with seven sides and seven angles. These seven sides can take various forms and lengths, making heptagons a diverse family of geometric shapes. The term “heptagon” is derived from the Greek words “hepta,” meaning seven, and “gonia,” meaning angle. Therefore, a heptagon is also referred to as a seven-sided polygon. In this comprehensive article, we will embark on a journey to understand heptagons, explore their properties, and unravel their significance in mathematics and the real world.
Table of Contents:
-
- What is a Heptagon?
- Properties of Heptagons
- Types of Heptagon
- Heptagon Diagonals
- Area of a Heptagon
- Perimeter of a Heptagon
- Solving with Heptagons: Practical Applications
- A Step-By-Step Guide to Heptagon Problems
Table of Contents
What is a Heptagon?
A heptagon is a polygon, which is a two-dimensional geometric shape, characterized by having seven sides and seven angles. Heptagons can vary in shape, and their sides and angles are not necessarily of equal length or measure. They are classified as irregular polygons because of this variation in side lengths and angle measures. Despite their irregularity, heptagons possess unique geometric properties and can be found in various mathematical and real-world contexts.
Understanding heptagons and their properties is valuable in geometry and can be applied in fields such as architecture, engineering, and design where polygonal shapes play a significant role.
Properties of Heptagons
Heptagons exhibit intriguing properties, including:
- Seven Sides and Angles: As a seven-sided polygon, heptagons have seven interior angles and seven sides.
- Sum of Interior Angles: The sum of the interior angles of a heptagon always equals 900 degrees.
- Irregular Nature: Heptagons do not have equal sides or equal angles, making them irregular polygons.
Types of Heptagon
Heptagons, or seven-sided polygons, can be categorized into different types based on their properties and characteristics. Here are some common types of heptagons:
- Regular Heptagon: A regular heptagon is a heptagon in which all seven sides and all seven angles are of equal length and measure. It is a symmetrical geometric shape.
- Irregular Heptagon: An irregular heptagon is a heptagon that does not have all sides or angles of equal length or measure. In other words, it lacks the symmetry of a regular heptagon.
- Convex Heptagon: A convex heptagon is a heptagon in which all of its interior angles are less than 180 degrees. It has no interior angles greater than 180 degrees, and its sides do not cross over each other.
- Concave Heptagon: A concave heptagon is a heptagon that has at least one interior angle greater than 180 degrees. It exhibits a “caved-in” or “dented” appearance, and its sides may intersect.
Heptagon Diagonals
Understanding the diagonals of a heptagon can aid in solving complex geometric problems. Explore the relationships and properties of these internal line segments.
Area of a Heptagon
Calculating the area of a heptagon, which is a seven-sided polygon, can be a bit more complex than finding the area of simpler shapes like triangles or rectangles. The formula to find the area of a regular heptagon, where all sides and angles are equal, involves some trigonometric calculations. Here’s how you can calculate the area of a regular heptagon:
Area of a Regular Heptagon (A):
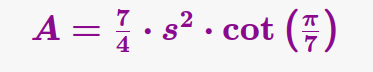
Where:
- A is the area of the heptagon.
- s is the length of one side of the heptagon.
- π is the mathematical constant pi (approximately 3.14159).
- cot(θ) represents the cotangent of the angleθ.
Perimeter of a Heptagon
To calculate the perimeter of a heptagon, you need to find the sum of the lengths of all seven sides. Since a heptagon has seven sides, let’s denote the lengths of the sides as a, b, c, d, e, f, and g. The perimeter (P) can be calculated as follows:
P = a + b + c + d + e + f + g
Simply add the lengths of all seven sides together to determine the perimeter of the heptagon. Make sure to use consistent units (e.g., centimeters, inches, meters) for accurate calculations.
FAQs
1. What is a heptagon in geometry?
A heptagon is a polygon with seven sides and seven angles. It is a seven-sided geometric shape with various properties and characteristics.
2. What are the key properties of heptagons?
Key properties of heptagons include having seven sides, seven interior angles, and a sum of interior angles equal to 900 degrees. Heptagons can be regular (with equal sides and angles) or irregular.
3. How do you find the area of a heptagon?
To find the area of a heptagon, you can use the formula for a regular heptagon: Area = (7/4) × s^2 × cot(π/7), where s is the length of one side. For irregular heptagons, you may need to divide them into smaller shapes and calculate their areas separately.
4. How is the perimeter of a heptagon calculated?
The perimeter of a heptagon is found by adding the lengths of all seven sides. It’s the sum of the side lengths that enclose the heptagon.
5. Are there different types of heptagons?
Yes, heptagons can be categorized into types based on their properties. Regular heptagons have equal sides and angles, while irregular heptagons do not. Heptagons can also be classified as convex or concave.
6. Where are heptagons used in the real world?
Heptagons have applications in various fields, including architecture, design, and art. They can be found in decorative patterns, architectural elements, and other design aspects.
7. How can I calculate the area of an irregular heptagon?
For irregular heptagons, you may need to split them into smaller shapes like triangles and trapezoids. Calculate the area of each component and then sum them to find the total area of the irregular heptagon.