Decimals are an essential part of the number system, and they are all around us in our daily lives. Whether you’re shopping, doing your homework, or measuring ingredients for a recipe, you encounter decimals regularly. In this article, we’ll explore what decimals are, how they work, and the various ways they’re used in different aspects of life.
Dividing decimals may seem a bit tricky at first, but it’s a fundamental math skill that’s incredibly useful in various real-life situations. In this tutorial, we’ll break down the process of dividing decimals step by step with clear examples.
Table of Contents
What Are Decimals?
Decimals are a way to express parts of a whole. They are numbers that fall between whole numbers. In the decimal system, we use the base 10, which means there are ten digits (0-9). A decimal number includes a whole number part and a fractional part, separated by a decimal point.
For example, in the number 3.141, “3” is the whole number part, and “.141” is the fractional part. This means we have 3 whole units and 141/1000 of another unit.
Understanding Decimal Place Value
One of the critical concepts in decimals is place value. Each digit in a decimal has a specific place and value. Let’s break down the number 3.141:
- The digit “1” is in the “thousands” place.
- The digit “4” is in the “hundreds” place.
- The digit “1” is in the “tens” place.
- The digit “4” is in the “ones” place.
- The digit “1” is in the “tenths” place.
- The digit “4” is in the “hundredths” place.
The place value of each digit tells us how much it contributes to the overall value of the number.
Decimals are used in a wide range of mathematical operations. You can add, subtract, multiply, and divide decimals just like whole numbers. However, you need to be mindful of the placement of the decimal point.
What is a dividend? What is a divisor?
- Dividend: The dividend is the number that is being divided. It is the quantity that you want to split into equal parts. In a division problem, the dividend is divided by the divisor to find the quotient.
- Divisor: The divisor is the number by which the dividend is divided. It represents the number of equal parts into which the dividend will be divided. The divisor tells you how many times the dividend will be split.
For example, in the division problem 12 ÷ 3 = 4:
- 12 is the dividend.
- 3 is the divisor.
- 4 is the quotient, which is the result of the division.
In this example, 12 (dividend) is divided by 3 (divisor) to obtain a quotient of 4. The division process involves finding out how many times the divisor can fit into the dividend evenly.
How to Divide Decimals by Whole Numbers
Let’s begin with an uncomplicated example that you may find solvable without resorting to long division (even though we’ll employ long division to provide a clear illustration of our 3-step process for dividing decimals).
For this example, as well as all those that will follow, you’ll be utilizing the subsequent three-step technique for dividing decimals:
Step One: Recognize the dividend and the divisor, and determine whether the divisor is a whole number (if it is, proceed to Step Three).
Step Two: If the divisor is not a whole number, modify it by multiplying it by a multiple of 10 to convert it into a whole number (e.g., multiply tenths by 10, hundredths by 100, thousandths by 1,000, and so forth). It’s important to note that whatever multiple of 10 you use to modify the divisor, you must also apply the same multiplication factor to the dividend.
Step Three: Execute the division operation employing the long division method to obtain the solution.
How to Divide Decimals by Whole Numbers
Example #1: 4.5 ÷3
Step 1: Identify the Dividend and Divisor
- The dividend is 4.5, the number you want to divide.
- The divisor is 3, a whole number, which means you can proceed to Step Three directly.

Step 2: Move the Decimal
To avoid working with decimals, you can shift the decimal point in the dividend to the right until it becomes a whole number. Simultaneously, move the decimal point in the answer (quotient) to the same position. Count the number of places you moved the decimal point.
In our example, move the decimal point in 4.5 one place to the right, making it 45. Also, move the decimal point in the answer one place to the right:

Step 3: Divide and Find the Quotient
Now, perform the division as you would with whole numbers. Divide 45 by 3:

45 divided by 3 equals 15. So, your quotient is 15:

Step 4: Add the Decimal Point
Finally, bring back the decimal point into your answer (quotient) in the same position as it was in the dividend:
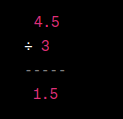
Conclusion
Dividing decimals by whole numbers is a straightforward process. Set up the division, move the decimal to the right to create a whole number, perform the division with whole numbers, and then reintroduce the decimal point into your quotient. Practice with different examples to become more confident in this skill.