A square is a fundamental geometric shape with unique properties that set it apart from other polygons. In this exploration of squares, we’ll delve into their shape, properties, how to calculate their area and perimeter, and the intriguing concept of the diagonal.
Table of Contents
What is a Square
A square is a quadrilateral, which means it has four sides. What distinguishes a square is that all four sides are of equal length, and all four angles are right angles (90 degrees). This makes the square a regular polygon, with symmetry and balance in its shape.
Properties of a Square
- Equal Sides: All four sides of a square are of the same length, making it a regular polygon.
- Right Angles: Each angle within a square is a right angle, measuring 90 degrees.
- Diagonals: The diagonals of a square bisect each other at 90-degree angles, dividing the square into four congruent right-angled triangles.
- Symmetry: Squares are symmetric shapes. You can rotate a square by 90 degrees, 180 degrees, or 270 degrees, and it will look the same.
Basic Formulas Related to Squares
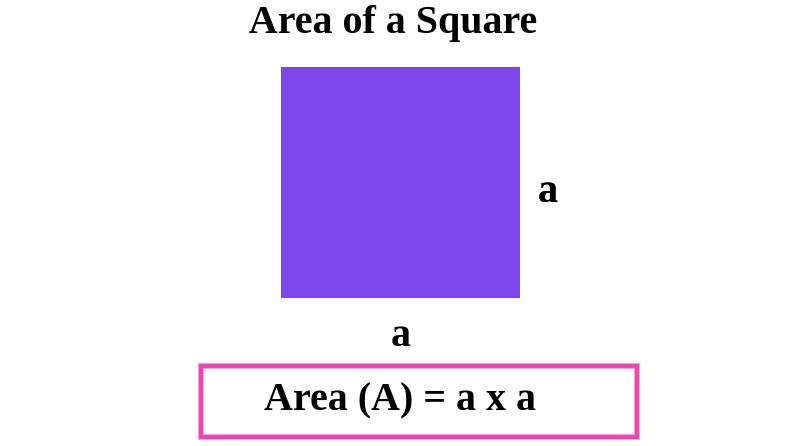
Area of a Square
The area of a square is calculated by multiplying the length of one of its sides by itself (squared). The formula is:
Area (A) = Side (a) x Side (a)
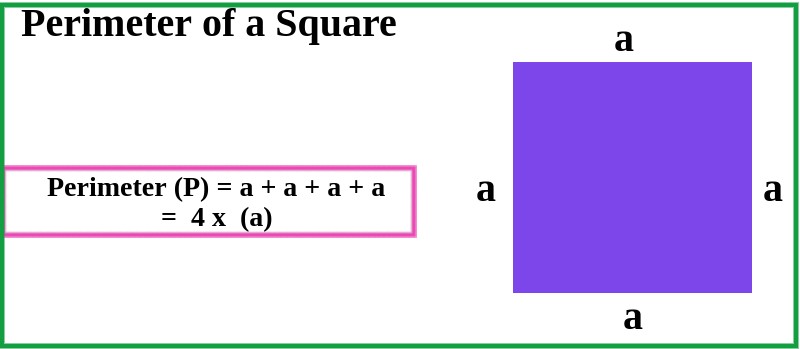
Perimeter of a Square
The perimeter of a square is the sum of all its sides. Since all sides are equal, you can simply multiply the length of one side by 4 to find the perimeter. The formula is:
Perimeter (P) = 4 x Side (a)
Diagonal of a Square
The diagonal of a square is a line segment connecting one corner of the square to the opposite corner. It divides the square into two congruent right-angled triangles. To calculate the length of the diagonal (d) when you know the side length (s), you can use the Pythagorean theorem:
d² = s² + s²
d² = 2s²
d = √(2s²)
d = s√2
The diagonal of a square is equal to the side length multiplied by the square root of 2.
Solved Examples on Square
Example 1: If the side length of a square is 6 cm, what is its area?
Solution:
- Use the formula for the area of a square: Area (A) = Side (s) x Side (s).
- Substitute the given side length: A = 6 cm x 6 cm = 36 square cm.
Example 2: Determine the perimeter of a square with a side length of 5 inches.
Solution:
- Use the formula for the perimeter of a square: Perimeter (P) = 4 x Side (s).
- Plug in the given side length: P = 4 x 5 inches = 20 inches.
Example 3: If the side length of a square is 10 meters, what is the length of its diagonal?
Solution:
- Use the formula for the diagonal of a square: Diagonal (d) = Side (s) x √2.
- Substitute the given side length: d = 10 meters x √2 ≈ 14.14 meters (rounded to two decimal places).
Example 4: Compare the areas of two squares. Square A has a side length of 7 cm, and Square B has a side length of 10 cm.
Solution:
- Use the area formula for both squares:
- Area of Square A = (7 cm) x (7 cm) = 49 square cm
- Area of Square B = (10 cm) x (10 cm) = 100 square cm
- Since 100 square cm is greater than 49 square cm, Square B has a larger area.
Example 5: A square has a perimeter of 36 meters. What is its area?
Solution:
- Use the formula for the perimeter of a square: Perimeter (P) = 4 x Side (s).
- Since the perimeter is 36 meters, you can find the side length: 4s = 36 m, so s = 36 m / 4 = 9 meters.
- Now, calculate the area using the side length: Area (A) = Side (s) x Side (s) = 9 m x 9 m = 81 square meters.
FAQs
1. What is a square in geometry?
A square is a four-sided polygon with all sides of equal length and all angles measuring 90 degrees. It’s a regular quadrilateral and one of the fundamental geometric shapes.
2. What’s the relationship between a square and a cube?
A square is a two-dimensional shape, while a cube is a three-dimensional figure. A cube has six square faces. Each face of a cube is a square.
3. How can I determine the side length of a square if I know its area?
To find the side length (s) of a square when you know its area (A), use the formula: s = √A. Take the square root of the area to find the side length.
4. What’s the difference between a square and a quadrilateral?
A square is a specific type of quadrilateral, which is a broad category of four-sided polygons. The key difference is that all sides of a square are equal in length and all angles are right angles, while a quadrilateral may have sides and angles of varying measures.
5. Can squares have negative side lengths?
In geometric contexts, squares are typically defined with positive side lengths. Negative side lengths do not align with the conventional definition of squares.
6. Are there different types of squares?
No, there is only one type of square in terms of its defining characteristics. All squares have equal sides and right angles.
Yes, a square is a specific type of rectangle.