Table of Contents
Is a Square a Rectangle?
The question of whether a square is a rectangle might seem straightforward, but it’s a topic that can lead to some interesting discussions in mathematics and geometry. To answer this question, we need to delve into the definitions and characteristics of squares and rectangles, and explore the relationships between these two fundamental geometric shapes.
What is a Square?
A square is a four-sided polygon, also known as a quadrilateral, in which all four sides are of equal length. Additionally, all four angles in a square are right angles, which means they measure 90 degrees. In simple terms, a square is a special type of rectangle in which all sides have the same length.
What is a Rectangle?
A rectangle, like a square, is a four-sided polygon with four right angles. However, in a rectangle, opposite sides are equal in length, but not all sides. This means that rectangles can have two pairs of sides with different lengths. This distinction sets rectangles apart from squares.
Understanding the Relationship between Square and Rectangle
So, is a square a rectangle?
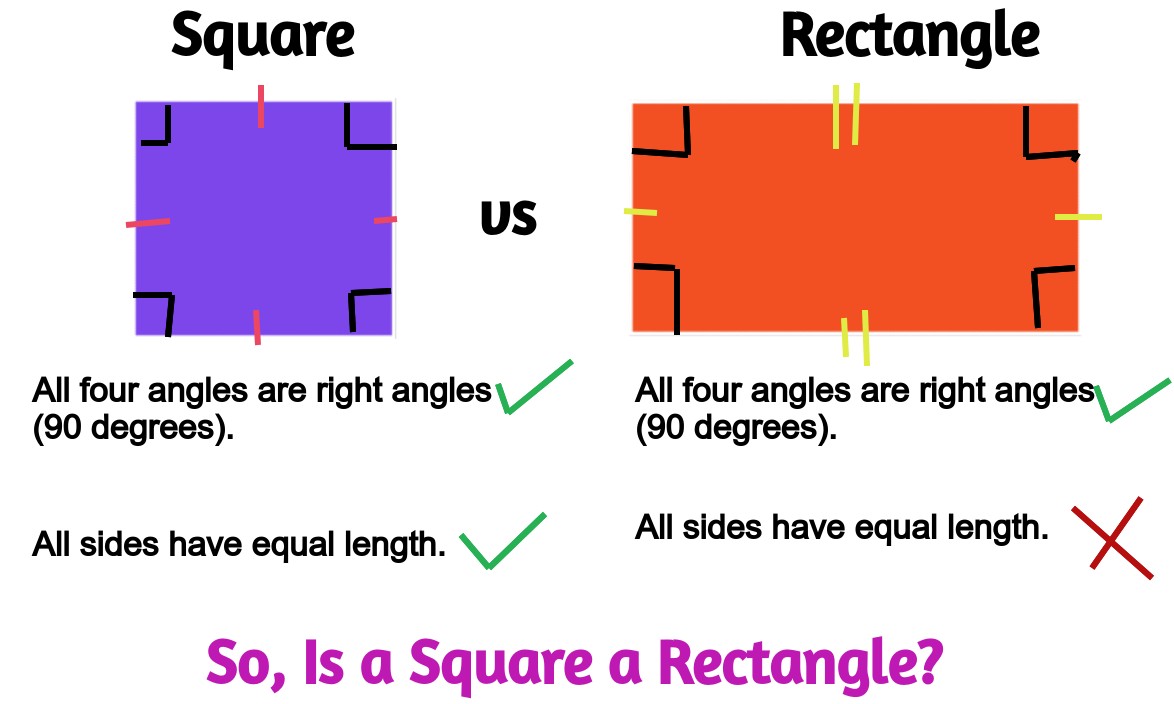
The answer is yes.
Every square is, in fact, a type of rectangle, but not every rectangle is a square. In other words, all squares share the fundamental characteristics of rectangles, including having four right angles. However, squares are unique in that all their sides are of equal length, making them a specific subset of rectangles.
Key Takeaways
- A square is a special type of rectangle, as it shares the same characteristic of having four right angles.
- In a square, all sides are of equal length, which distinguishes it from a general rectangle.
- Rectangles have two pairs of sides with different lengths, while squares have all sides of equal length.
- Understanding the relationships between geometric shapes helps us classify and work with them more effectively in mathematics and real-world applications.
In summary, squares and rectangles are closely related geometric shapes. A square is a type of rectangle due to its right angles, but it’s distinct in that all its sides are equal in length. This exploration highlights the nuances of geometry and provides insights into the classification of shapes, demonstrating how mathematical concepts can be both precise and intriguing.