How to Find the Vertex of a Parabola

A parabola is a special kind of curve that looks like a smiley face or a frowny face! It can also look like a rainbow or even a water slide. Parabolas are all around us, and they have some really interesting secrets to share.

The Shape of Joy! Imagine drawing half of a heart and then flipping it over. That’s a parabola! It’s super symmetrical, which means it’s perfectly balanced. If you cut a parabola in half, each side is a mirror image of the other. That’s what makes parabolas so special.

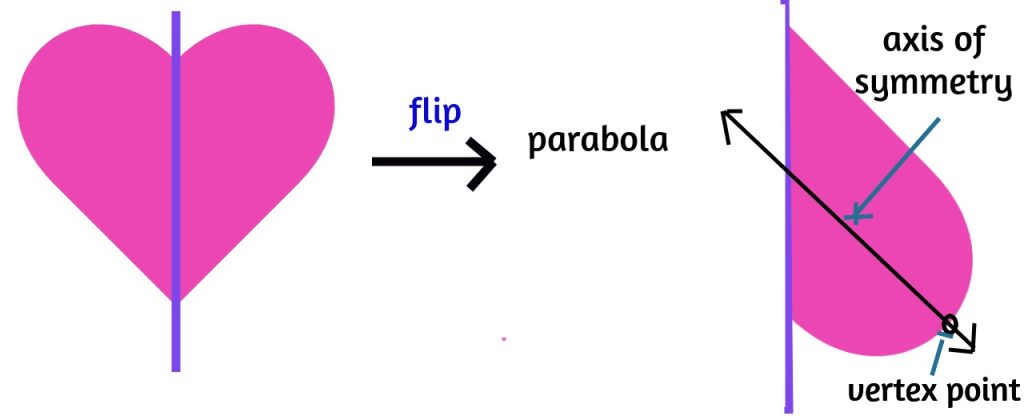
Table of Contents

What is a parabola?

A parabola is a geometric shape that can be described as a symmetrical curve with a U-like or arch-like appearance. It’s one of the fundamental curves in mathematics, often encountered in various real-world scenarios. The term “parabola” is derived from the Greek word “parabole,” which means “comparison.”

In simple terms, a parabola is defined by a quadratic equation of the form y = ax² + bx + c, where “a,” “b,” and “c” are constants, and “x” and “y” are variables. The key characteristics of a parabola include:

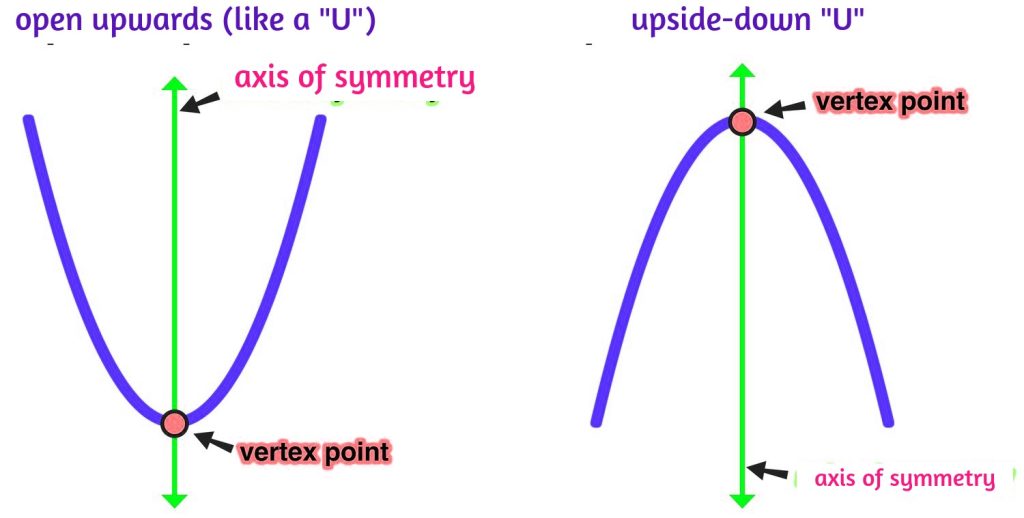
Symmetry: A parabola is symmetric about an axis called the “axis of symmetry,” which is a vertical line that passes through the vertex, the highest or lowest point on the parabola.
Vertex: The vertex is the highest or lowest point on the parabola, and it lies on the axis of symmetry. The coordinates of the vertex are typically denoted as (h, k).
Direction: A parabola can open upwards (like a “U”) if “a” is positive, or it can open downwards (like an upside-down “U”) if “a” is negative.
Focal Point and Directrix: A parabola also has a focal point and a directrix. All points on the parabola are equidistant to the focal point and the directrix. The focal point is located inside the curve.

What is the vertex of a parabola?

Think of a parabola as a curve that looks like a smiley face or a frowny face. The vertex is like the nose of the smiley or frowny face. It’s the point right in the middle, and it’s very special because it’s the highest or lowest point on the curve, depending on whether the curve is smiling (opening up) or frowning (opening down).

The vertex also helps us understand where the parabola is divided into two equal halves, like a mirror right down the middle. We call this line the “axis of symmetry,” and the vertex is where the parabola touches that line.

In math, we use (h, k) to talk about the vertex. “h” tells us where the vertex is left or right, and “k” tells us how high or low it is. So, the vertex is like the most special point on the parabola, and it helps us understand how the curve looks and where it’s balanced. It’s kind of like the nose of the parabola’s face!

What is the formula for the vertex of a parabola?

To find the precise coordinates of the vertex, we employ a formula that relates to the coefficients of the quadratic equation. For a parabola in standard form, y = ax² + bx + c, the x-coordinate of the vertex, denoted as “h,” is determined by the formula:

This formula tells us that the x-coordinate of the vertex lies at the midpoint of the axis of symmetry, and it is obtained by taking the opposite of the coefficient “b” and dividing it by twice the coefficient “a.” This is a vital step in pinpointing the vertex.

The y-coordinate of the vertex, denoted as “k,” is found by substituting the x-coordinate “h” back into the original equation:

k = a(h)² + b(h) + c

By applying these formulas, you can precisely identify the coordinates of the vertex (h, k), which define the vertex’s position on the parabolic curve.

Type of Parabola	General Equation	Vertex Formula	Vertex (h, k)
Upward (a > 0)	y = ax² + bx + c	(-b/2a, c – b²/4a)	(h, k)
Downward (a < 0)	y = ax² + bx + c	(-b/2a, c – b²/4a)	(h, k)

In the table:

“Type of Parabola” specifies whether the parabola opens upward (a > 0) or downward (a < 0).
“General Equation” is the standard form of the parabola equation.
“Vertex Formula” provides the formula to calculate the x-coordinate (h) and y-coordinate (k) of the vertex.
“Vertex (h, k)” shows the vertex’s coordinates.

For an upward-opening parabola, the vertex is at the point (-b/2a, c – b²/4a), and for a downward-opening parabola, it is at the same coordinates. The only difference between the two types is the sign of ‘a’ in the equation.