In mathematics, “reflection” refers to a transformation that flips a geometric figure over a mirror line or axis. This transformation creates a mirror image of the original figure. The mirror line or axis, known as the “line of reflection,” serves as the axis of symmetry, and each point on the original figure is mapped to an equivalent point on the reflected figure, maintaining the same distance from the line of reflection.

Key points about reflection in math:
- Line of Reflection: The line or axis over which the reflection occurs is crucial. It can be horizontal, vertical, or diagonal, depending on the desired transformation.
- Preservation of Distances: In a reflection, the distance between any point on the original figure and the line of reflection is the same as the distance between the corresponding point on the reflected figure and the same line.
- Symmetry: Reflection creates symmetry. If a figure is reflected over a line, the result is a figure that is symmetric with respect to that line.
- Notation: Reflection is often denoted using the symbol “R,” followed by the axis of reflection. For example, “R_x” signifies a reflection over the x-axis.
Table of Contents
Math Definition: Reflection Over the X Axis
In mathematics, “reflection over the x-axis” is a geometric transformation that involves flipping a point, a shape, or an object over the x-axis, which is the horizontal axis on the Cartesian coordinate system. This transformation creates a new point, shape, or object on the opposite side of the x-axis while maintaining the same distance from the x-axis.

Key points about reflection over the x-axis:
- Symmetry: Reflecting over the x-axis results in a new object that is symmetric to the original with respect to the x-axis. If a point is (x, y), its reflected point is (x, -y).
- Axis of Reflection: The x-axis serves as the line of reflection, also known as the axis of reflection. Points on the x-axis remain fixed in position during the reflection.
- Coordinates: When reflecting a point (x, y) over the x-axis, the x-coordinate remains the same, and the y-coordinate changes sign (positive to negative or negative to positive).
For example, Let’s take a point A(2, 3) and illustrate the reflection over the x-axis:
Original Point A(2, 3)

Reflected Point A'(2, -3)
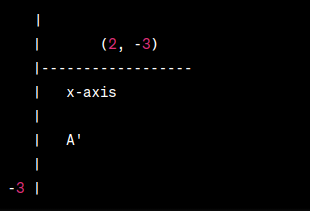
In the diagram, you can see point A(2, 3) reflected over the x-axis to point A'(2, -3). The x-coordinate remains the same, and the y-coordinate changes sign. This demonstrates the reflection over the x-axis, which results in a symmetric point with respect to the x-axis.
Math Definition: Reflection Over the Y Axis
In mathematics, “reflection over the y-axis” is a geometric transformation that involves flipping a point, a shape, or an object over the y-axis, which is the vertical axis on the Cartesian coordinate system. This transformation creates a new point, shape, or object on the opposite side of the y-axis while maintaining the same distance from the y-axis.
Key points about reflection over the y-axis:
- Symmetry: Reflecting over the y-axis results in a new object that is symmetric to the original with respect to the y-axis. If a point is (x, y), its reflected point is (-x, y).
- Axis of Reflection: The y-axis serves as the line of reflection, also known as the axis of reflection. Points on the y-axis remain fixed in position during the reflection.
- Coordinates: When reflecting a point (x, y) over the y-axis, the y-coordinate remains the same, and the x-coordinate changes sign (positive to negative or negative to positive).
For example, if you have a point B(3, 4) and you want to reflect it over the y-axis, the reflected point would be (-3, 4). This transformation is fundamental in geometry and has applications in various mathematical and scientific fields, including physics and computer graphics.