The world of geometry is a treasure trove of fascinating shapes, each with its unique properties and applications. One such shape, the rhombus, is a quadrilateral that has intrigued mathematicians, artists, and engineers alike for centuries. In this comprehensive guide, we will explore the rhombus from every angle, providing a deep understanding of its definition, properties, real-world applications, and even a step-by-step tutorial on how to draw and work with rhombi in various contexts.
Table of Contents:
- The Rhombus Unveiled
- Properties of a Rhombus
- Real-World Rhombus Examples
- Angles of Rhombus
- Rhombus Formulas
- Rhombus Examples
Table of Contents
What is Rhombus?
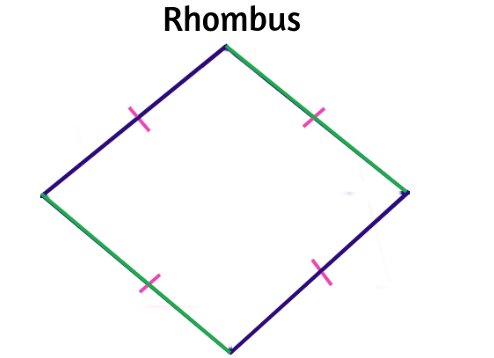
A rhombus is a quadrilateral, a four-sided polygon, with several unique characteristics that distinguish it from other shapes. Its defining feature is that all four sides are equal in length, and its opposite angles are equal. In other words, a rhombus is a parallelogram with all sides of equal length.
Properties of a Rhombus
Rhombi are known for their remarkable properties, including:
- Equal Side Lengths: All four sides of a rhombus are of equal length.
- Opposite Angles: The opposite angles of a rhombus are equal.
- Diagonals: The diagonals of a rhombus are perpendicular and bisect each other.
- Area and Perimeter: Formulas for calculating the area and perimeter of a rhombus.
Real-World Rhombus Examples
Rhombi are not confined to the world of mathematics; they are prevalent in everyday life and various industries. Some real-world examples include:
- Diamonds: Many precious stones, including diamonds, are cut into the shape of a rhombus, showcasing their brilliance.
- Kites: Kite-flying enthusiasts are familiar with the rhombus-shaped kites that soar in the sky.
- Mosaic Patterns: In interior design and architecture, rhombus-shaped tiles are used to create visually striking patterns.
- Engineering: Rhombi play a crucial role in the construction of trusses and other structural elements.
Angles of Rhombus
The angles of a rhombus have some distinctive properties:
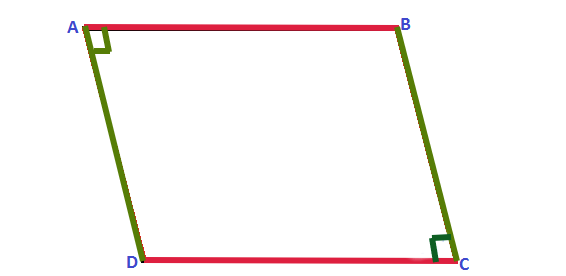
- Opposite Angles: The opposite angles of a rhombus are equal. In other words, if you label the angles of a rhombus as A, B, C, and D, then angle A is equal to angle C, and angle B is equal to angle D.
- Interior Angles: The sum of the four interior angles of a rhombus is always 360 degrees. This means that when you add up all the angles inside a rhombus, their total will be 360 degrees.
- Right Angles: The diagonals of a rhombus bisect each other at right angles. This means that the angles formed where the diagonals meet are all right angles (90 degrees).
- Adjacent Angles: The adjacent angles (angles that share a side) in a rhombus are supplementary, meaning the sum of the two adjacent angles is always 180 degrees.
These angle properties make rhombi particularly interesting and useful in various geometric and mathematical contexts.
Rhombus Formulas
1. Area of a Rhombus
The area (A) of a rhombus can be calculated using the formula:
Area of Rhombus, A = (d1 x d2)/2 square units
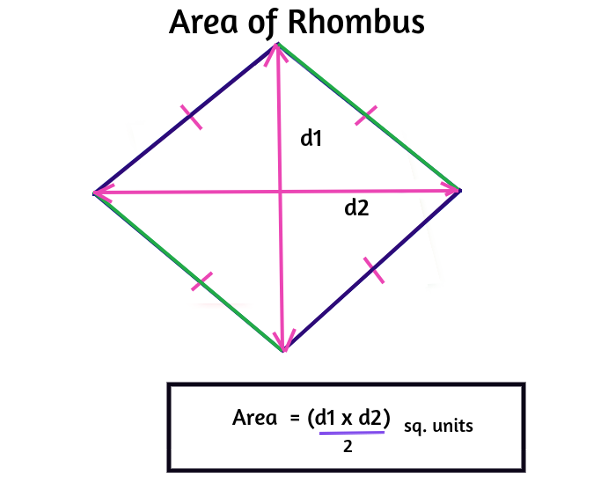
Where:
- d1 is the length of one diagonal.
- d2 is the length of the other diagonal.
2. Perimeter of a Rhombus
The perimeter (P) of a rhombus is found by multiplying the length of one of its sides (s) by 4:
Perimeter of a Rhombus P = 4s
Where:
- s is the length of one side.
3. Diagonal Lengths in a Rhombus
The lengths of the diagonals in a rhombus can be calculated using the Pythagorean Theorem. If s is the length of one side, then the lengths of the diagonals d1 and d2 are given by:
d1 =s √ 2
d2 =s √ 2
Here √ 2 represents the square root of 2.
These formulas are essential for solving problems involving the area, perimeter, and diagonal lengths of rhombi in various mathematical and practical applications.
Rhombus Examples
Example 1: Given a rhombus with diagonals of length 8 inches and 6 inches, calculate its area.
Solution:
Diagonal, d1 = 8 inches, and d2 = 6 inches
A = (d1 × d2)/2
Area = (8×6)/2= 48/2
A = 24 sq. inches
Answer: The area of the rhombus = 25 sq. inches.
Example 2: If the side length of a rhombus is 10 centimeters, find its perimeter.
Solution: To find the perimeter of the rhombus, you can use the formula:
Length of the tile = 10 centimeters.
Perimeter= 4s
Substitute the side length:
Perimeter = 4 × side = 4 × 10 = 40
So, the perimeter of the rhombus is 40 centimeters.
FAQs
Q1: What is a rhombus?
A1: A rhombus is a quadrilateral, a four-sided polygon, in which all four sides are of equal length, and the opposite angles are equal.
Q2: What are the properties of a rhombus?
A2: Key properties of a rhombus include equal side lengths, equal opposite angles, diagonals that bisect each other at right angles, and adjacent angles that are supplementary.
Q3: How do I calculate the area of a rhombus?
A3: You can find the area of a rhombus using the formula: Area = (diagonal 1 * diagonal 2) / 2, where the diagonals are the line segments that cross the rhombus from corner to corner.
Q4: What is the perimeter of a rhombus?
A4: The perimeter of a rhombus is four times the length of one of its sides. You can calculate it using the formula: Perimeter = 4s, where “s” is the length of one side.
Q5: Are squares rhombi?
A5: Yes, squares are a specific type of rhombus where all sides are equal in length, and all angles are right angles.
Q6: Where can I find rhombi in the real world?
A6: Rhombi can be found in diamond shapes, kite designs, tiles in mosaics, and architectural patterns, among other places.
Q7: What is the relationship between the diagonals in a rhombus?
A7: The diagonals of a rhombus are perpendicular to each other and bisect each other, meaning they intersect at their midpoints.