A parallelogram is a two-dimensional geometric figure characterized by its four sides, forming a quadrilateral. What distinguishes a parallelogram is that its opposite sides are not only parallel but also of equal length. Additionally, the sum of adjacent angles within a parallelogram always totals 180 degrees.
In the realm of geometry, a diverse array of 2D shapes and sizes, such as circles, squares, rectangles, rhombi, and more, exists. Each of these shapes boasts its unique set of properties. Furthermore, their area and perimeter formulas differ, serving as valuable tools for solving a wide range of mathematical problems. In this exploration, we will delve into the definition, properties, and formulas that govern parallelograms, shedding light on this intriguing geometric entity.
Table of Contents:
- Parallelogram Definition
- Properties of Parallelograms
- Calculating the Area of a Parallelogram
- Finding the Perimeter of a Parallelogram
- Solved Examples: Applying Parallelogram Concepts
- Real-World Applications
- A Step-by-Step Tutorial: Navigating the World of Parallelograms
Table of Contents
Parallelogram Definition
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. The name “parallelogram” originates from the Greek words “parallelos” (meaning parallel) and “gramma” (meaning a line or something written). This defines the essence of the shape – parallel lines.
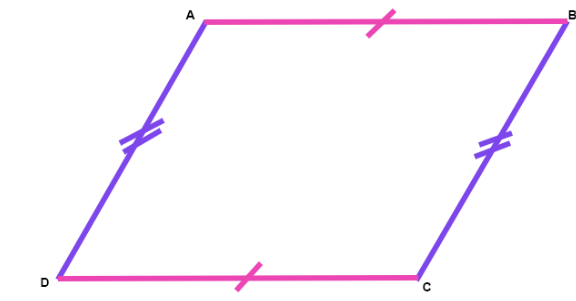
Properties of Parallelogram
Parallelograms exhibit a range of unique properties, including:
- Opposite Sides: Opposite sides are equal in length and parallel.
- Opposite Angles: Opposite angles are equal.
- Consecutive Angles: Consecutive angles are supplementary (their sum is 180 degrees).
- Diagonals: The diagonals of a parallelogram bisect each other.
Area of a Parallelogram
The area of a parallelogram can be determined using the formula:
Area= Base × Height
Where:
- The base is the length of one of the parallel sides.
- The height is the perpendicular distance between the two parallel sides.
Perimeter of a Parallelogram
To calculate the perimeter of a parallelogram, you add the lengths of all its sides:
Perimeter= 2(Side1+ Side2)
Types of Parallelogram
Parallelograms come in various types, and their classification is based on specific properties and characteristics. Here are some common types of parallelograms:
- Rectangle: A rectangle is a type of parallelogram with all right angles (90 degrees). It has opposite sides that are parallel and equal in length.
- Square: A square is a special type of rectangle, and thus a parallelogram, with all sides of equal length and all angles measuring 90 degrees.
- Rhombus: A rhombus is a parallelogram with all sides of equal length. While its opposite angles are equal, they are not necessarily right angles.
- Kite: A kite is a type of quadrilateral where two pairs of adjacent sides are of equal length. It may or may not have opposite sides that are parallel.
- Isosceles Trapezoid: An isosceles trapezoid is a parallelogram with one pair of opposite sides that are parallel, and the other pair of opposite sides of different lengths.
- Arrowhead Parallelogram: Also known as an arrowhead shape, this parallelogram has one pair of parallel sides and unequal adjacent sides. It somewhat resembles an arrowhead.
Is Square a Parallelogram?
Yes, a square is a type of parallelogram. In fact, a square is a specific and special case of a parallelogram.
By definition, a parallelogram is a quadrilateral (a polygon with four sides) with opposite sides that are both parallel and of equal length. A square not only has these properties, but it also has the additional feature that all of its angles are right angles (90 degrees). In other words, a square is a parallelogram with all right angles.
So, while a square is a parallelogram, not all parallelograms are squares.
Is Rectangle a Parallelogram?
Yes, a rectangle is a type of parallelogram. By definition, a parallelogram is a quadrilateral with opposite sides that are parallel and of equal length. A rectangle fulfills these criteria, as it has opposite sides that are parallel to each other and equal in length.
In addition to being a parallelogram, a rectangle has the special property of having all its angles equal to 90 degrees (right angles). This makes it a particular type of parallelogram with the additional characteristic of right angles, which is why rectangles are often considered separately from general parallelograms.
Examples on Parallelogram
Example 1: Given a parallelogram with a base of 8 inches and a height of 5 inches, calculate its area.
Solution: To find the area of the parallelogram, you can use the formula:
Area = Base x Height
Given, Base = 5 cm and Height = 8 cm.
Area = 5 × 8
Area = 40 Sq.cm
Example 2: If the length of one side of a parallelogram is 12 centimeters and the length of the other side is 8 centimeters, calculate its perimeter.
Solution:
To calculate the perimeter of the parallelogram, you can add the lengths of all its sides:
Perimeter= 2(Side1 + Side2)
Substitute the side lengths:
Perimeter= 2(12 centimeters+ 8 centimeters)= 2(20 centimeters) =40 centimeters
So, the perimeter of the parallelogram is 40 centimeters.