Unlocking the World of Trapezoid: Definition, Formulas, and Practical Applications
Trapezoid is intriguing geometric shapes that play a significant role in the realm of mathematics, engineering, and everyday life. In this comprehensive guide, we’ll delve into the definition, properties, area, and perimeter of trapezoid. Additionally, we’ll explore a variety of solved examples to illustrate their practical application. Whether you’re a student aiming to master geometry or a professional seeking real-world insights, this guide has something to offer.
Table of Contents:
- What is a Trapezoid?
- Properties of Trapezoids
- Calculating the Area of a Trapezoid
- Finding the Perimeter of a Trapezoid
- Solved Examples: Applying Trapezoid Concepts
- Shape of Trapezoids
- A Step-By-Step Tutorial: Navigating Trapezoidal Challenges
Table of Contents
What is a Trapezoid?
A trapezoid is a quadrilateral with one pair of opposite sides that are parallel. This distinctive feature sets it apart from other quadrilaterals and opens the door to a range of intriguing properties and applications.
Types of Trapezoids
Trapezoid can be categorized into different types based on their properties and the lengths of their sides and angles. The main types of trapezoids include:
- Isosceles Trapezoid: In an isosceles trapezoid, the two non-parallel sides (the legs) are of equal length. This type of trapezoid has two equal base angles and two equal non-base angles.
- Right Trapezoid: A right trapezoid is characterized by one right angle (a 90-degree angle). This right angle forms at the intersection of one of the legs and one of the bases.
- Scalene Trapezoid: A scalene trapezoid has no sides of equal length, meaning all four sides have different lengths. The angles in a scalene trapezoid are also different from each other.
- Obtuse Trapezoid: In an obtuse trapezoid, one of the angles is obtuse, meaning it measures more than 90 degrees. The other three angles may be acute (less than 90 degrees) or right angles.
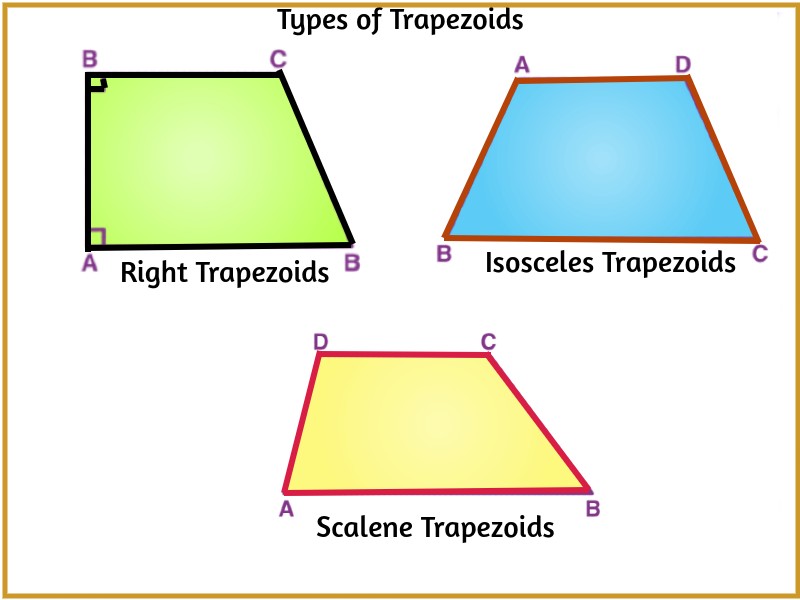
Shape of Trapezoids
A trapezoid is a four-sided geometric shape, classified as a quadrilateral. It is characterized by the following key features:
- Four Sides: A trapezoid has four sides or edges.
- Two Parallel Sides (Bases): Two of its sides are parallel to each other, and these are often referred to as the “bases.” The longer base is typically paired with the shorter base, but they can switch roles depending on the trapezoid’s orientation.
- Two Non-Parallel Sides (Legs): The other two sides are not parallel to each other and are called the “legs.” These legs may have different lengths.
- Four Vertices (Corners): Trapezoids have four corners or vertices where the sides meet.
- Internal Angles: A trapezoid has four internal angles formed at the intersections of its sides. These angles may vary in size depending on the specific trapezoid, but their sum is always 360 degrees.
The shape of a trapezoid can vary widely, from long and narrow to more balanced, depending on the lengths of its sides and the size of its angles. Its defining characteristic is the presence of one pair of parallel sides and one pair of non-parallel sides, which gives it a distinct geometric identity.
Area of a Trapezoid
The area of a trapezoid can be determined using the formula:
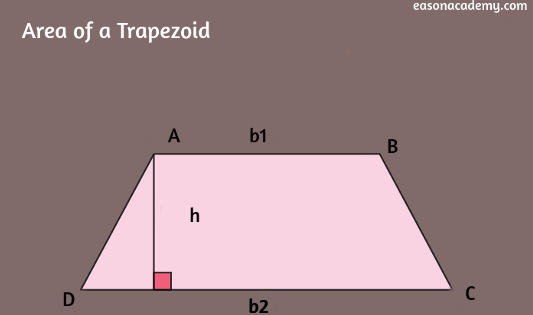
Area= 1/2× (Sum of the Lengths of the Parallel Sides) × Height
or
Area= 1/2 x (b1 +b2 ) × h
Where:
- The height is the perpendicular distance between the two parallel sides.
Perimeter of a Trapezoid
The perimeter of a trapezoid is the sum of the lengths of all its sides. A trapezoid has four sides: two parallel sides (the bases) and two non-parallel sides (the legs).
To calculate the perimeter, you can use the following formula:
Perimeter = a + b + c + d
Where:
- a and b are the lengths of the two parallel bases.
- c and dd are the lengths of the two non-parallel sides (the legs).
Simply add the lengths of these four sides to find the perimeter of the trapezoid.
Properties of Trapezoids
Trapezoids come with several key properties, including:
- One Pair of Parallel Sides: Trapezoids have one pair of opposite sides that are parallel.
- Diagonals: The diagonals of a trapezoid may have different lengths.
- Adjacent Angles: The adjacent angles in a trapezoid are supplementary, with their sum equaling 180 degrees.
Solved Examples
Example 1: Given a trapezoid with a longer base (b1) of 10 inches, a shorter base (b2) of 6 inches, and a height (h) of 4 inches, calculate its area.
Solution: To find the area of the trapezoid, you can use the formula:
Area= 1/2× (Sum of the Lengths of the Parallel Sides) × Height
Area= 1/2 (b1 +b2 ) × h
Area = (10+6)/2 × 4 (inches2) = 16/2 x 4 (inches2)
32 square inches
So, the area of the trapezoid is 32 square inches.
Example 2:If the lengths of the two bases are 12 centimeters and 8 centimeters, and the lengths of the legs are 5 centimeters each, calculate the perimeter of the trapezoid.
Solution:
To calculate the perimeter of the trapezoid, you can add the lengths of all its sides:
Perimeter = a + b + c + d
Substitute the base lengths (b1 and b2) and leg lengths (a and c):
Perimeter= 12 centimeters +8 centimeters +5 centimeters +5 centimeters = 30 centimeters
So, the perimeter of the trapezoid is 30 centimeters.
FAQs
1. What is a trapezoid?
A trapezoid is a four-sided geometric shape characterized by having two parallel sides (the bases) and two non-parallel sides (the legs). It is a type of quadrilateral.
2. How can I calculate the area of a trapezoid?
You can calculate the area of a trapezoid using the formula: Area = 1/2 × (sum of the lengths of the bases) × height. Make sure the height is perpendicular to the bases.
3. What is the perimeter of a trapezoid?
The perimeter of a trapezoid is the sum of the lengths of all its sides. It can be calculated by adding the lengths of the two bases and the two legs.
4. What types of trapezoids are there?
Trapezoids can be classified into types such as isosceles trapezoids (with equal leg lengths), right trapezoids (with one right angle), scalene trapezoids (with no equal sides or angles), obtuse trapezoids (with one obtuse angle), and acute trapezoids (with all acute angles).
5. What are the properties of a trapezoid?
Key properties of a trapezoid include having one pair of parallel sides, opposite angles that are supplementary (their sum is 180 degrees), and the diagonals that may have different lengths.
6. What’s the difference between a trapezoid and a parallelogram?
The key difference is that a trapezoid has one pair of parallel sides, while a parallelogram has both pairs of opposite sides parallel. Additionally, in a trapezoid, the opposite sides are not necessarily of equal length, while in a parallelogram, they are.
7. Can a rectangle be considered a trapezoid?
Yes, a rectangle can be classified as a trapezoid. A rectangle is a specific type of trapezoid with two pairs of opposite sides that are parallel and all right angles.