Geometry, a branch of mathematics, provides us with the tools to explore and understand the properties of shapes and figures in our two-dimensional world. In this article, we’ll embark on a journey into the captivating realm of 2D shapes, where we’ll discover their characteristics, common types, and real-world applications.
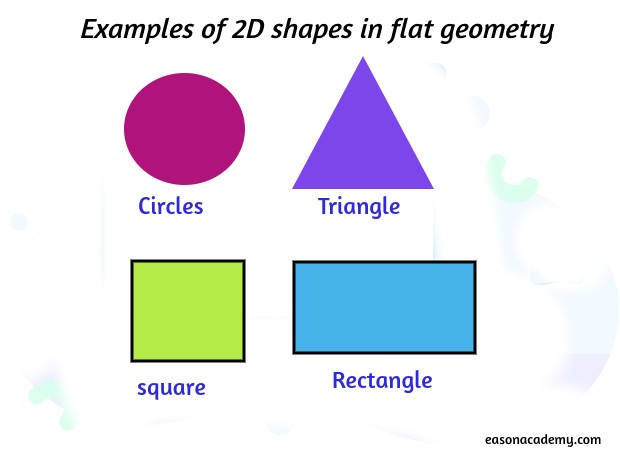
Table of Contents
What Are 2D Shapes?
Two-dimensional (2D) shapes are flat, planar figures that exist in two dimensions: length and width. Unlike three-dimensional (3D) objects that have depth, 2D shapes are entirely flat and have no thickness. These shapes are fundamental in geometry and are often encountered in everyday life.
2D Shapes Definition
In math, 2D shapes are defined as plane figures that can be illustrated on a flat or planar surface, such as a sheet of paper. These shapes encompass various parameters, including area and perimeter. While certain 2D shapes are characterized by straight sides and corners, others boast curved boundaries.
All 2D shapes feature sides, vertices (corners), and interior angles, except for the circle, which is a curved figure. Shapes with a minimum of three straight sides are classified as polygons, encompassing triangles, squares, and quadrilaterals. The figure below illustrates a common array of 2D shapes frequently encountered.
2D Shapes Names
2D shapes, also known as two-dimensional shapes, come in various forms and sizes. Here are some common 2D shape names:
1. Circle
The circle is a perfectly round shape with all points equidistant from its center. It is defined by its radius, which is the distance from the center to any point on its boundary. Circular shapes can be found in nature, such as the sun, and in everyday objects like wheels.
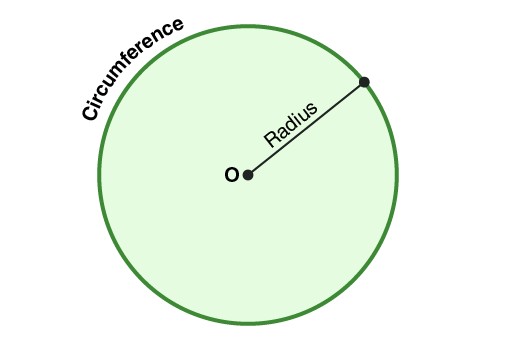
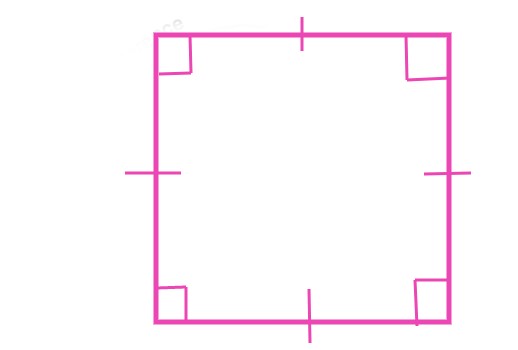
2. Square
A square is a four-sided polygon with all sides of equal length and all angles measuring 90 degrees. It is a regular polygon, and its symmetrical nature makes it a fundamental shape in geometry. Squares are often encountered in tiles, frames, and building structures.
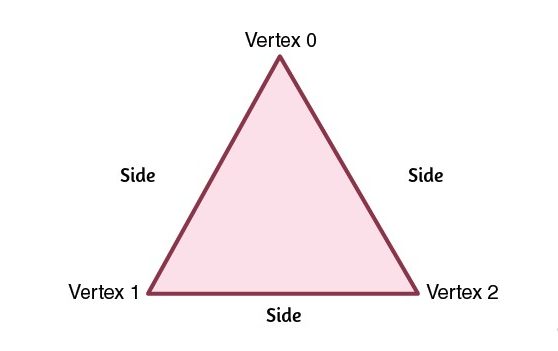
3. Triangle
A triangle is a polygon with three sides and three angles. There are various types of triangles, including equilateral (all sides and angles equal), isosceles (two sides and angles equal), and scalene (no sides or angles equal). Triangles are integral to trigonometry and serve as the basis for understanding angles and proportions.
4. Rectangle
A rectangle is a four-sided polygon with opposite sides of equal length and all angles measuring 90 degrees. Rectangles are prevalent in architecture and design, often seen in doors, windows, and picture frames.
5. Pentagon
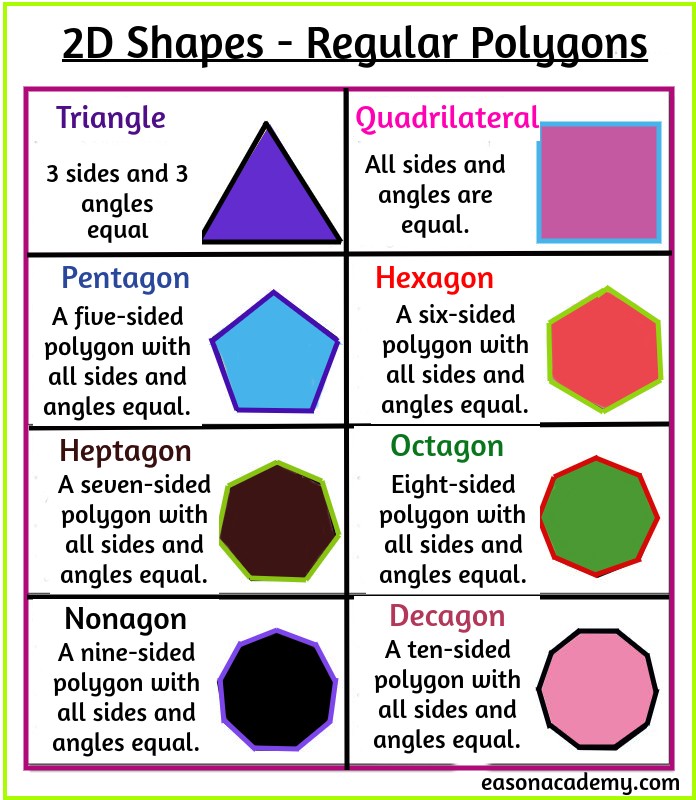
A pentagon is a five-sided polygon with five angles. Common types of pentagons include regular (all sides and angles equal) and irregular (sides and angles vary). The Pentagon building in Washington, D.C., is an example of a regular pentagon.
6. Hexagon
Hexagons have six sides and six angles. They are known for their efficiency in tessellation, as seen in honeycomb patterns. Hexagons are also present in bolts and nuts.
7. Octagon
Octagons are eight-sided polygons with eight angles. Their distinctive shape is often used in signs, such as stop signs, and in various architectural designs.
These are just a few examples of 2D shape names, but there are many more, each with its unique characteristics and properties.
2D Shapes Properties
Here’s a table summarizing the properties of common 2D shapes:
| Shape | Description | Properties |
|---|---|---|
| Circle | Perfectly round, no angles or sides | Constant radius, no angles |
| Square | Four equal sides, four right angles | Equal side lengths, 4 right angles |
| Rectangle | Four sides, opposite sides equal | Opposite sides equal, 4 right angles |
| Triangle | Three sides, three angles | Varying side lengths, 3 angles |
| Pentagon | Five sides, five angles | Varying side lengths, 5 angles |
| Hexagon | Six sides, six angles | Varying side lengths, 6 angles |
| Octagon | Eight sides, eight angles | Varying side lengths, 8 angles |
| Rhombus | Four equal sides, no right angles | Equal side lengths, no right angles |
| Oval | Elliptical, elongated shape | No angles, no equal sides |
| Parallelogram | Four sides, opposite sides parallel | Opposite sides parallel, no equal sides |
| Trapezoid | Four sides, one pair parallel | One pair parallel, no equal sides |
| Kite | Four sides, two pairs of adjacent sides with equal length | Two pairs of adjacent sides with equal length, no right angles |
| Heptagon | Seven sides, seven angles | Varying side lengths, 7 angles |
| Nonagon | Nine sides, nine angles | Varying side lengths, 9 angles |
| Decagon | Ten sides, ten angles | Varying side lengths, 10 angles |
Area and Perimeter of 2D Shapes
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Circle | πr² (where r is the radius) | 2πr (where r is the radius) |
| Square | side² (where side is the length of a side) | 4 × side (where side is the length of a side) |
| Rectangle | length × width | 2 × (length + width) |
| Triangle | 0.5 × base × height | Sum of the lengths of all three sides |
| Pentagon | (0.25 × (√5 × (5 + 2√5)) × side²) | 5 × side |
| Hexagon | (3/2) × (√3 × side²) | 6 × side |
| Octagon | 2 × side × (1 + √2) | 8 × side |
| Rhombus | (1/2) × product of diagonals | 4 × side (where side is the length of a side) |
| Oval | π × major radius × minor radius | No simple formula |
| Parallelogram | base × height | 2 × (base + side) |
| Trapezoid | (0.5 × (sum of bases) × height) | Sum of all sides |
| Kite | (1/2) × product of diagonals | Sum of all sides |
| Heptagon | (0.25 × 7 × side²) | 7 × side |
| Nonagon | (0.25 × 9 × side²) | 9 × side |
| Decagon | (0.25 × 10 × side²) | 10 × side |
2d Shapes and 3d Shapes
here’s a table comparing 2D shapes and 3D shapes:
| Shape Type | Description | Examples |
|---|---|---|
| 2D Shapes | Flat geometric figures with only length and width dimensions | Circle, Square, Triangle, Rectangle |
| 3D Shapes | Geometric objects with length, width, and height dimensions, possessing volume | Sphere, Cube, Pyramid, Cylinder |
2D Shapes Examples
Example 1 -Let’s find the area of a rectangle with a length of 8 units and a width of 5 units.
Solution:
The formula for the area of a rectangle is length × width. Substituting the given values:
Area = 8 units × 5 units = 40 square units.
Example 2 – Calculate the perimeter of an equilateral triangle with a side length of 6 centimeters.
Solution:
The perimeter of a triangle is the sum of its three sides. In an equilateral triangle, all sides are equal. So, the perimeter is:
Perimeter = 6 cm + 6 cm + 6 cm = 18 centimeters.
Example 3 -Determine the area of a circle with a radius of 3.5 meters.
Solution:
The formula for the area of a circle is πr², where “r” is the radius. Substituting the given value:
Area = π × (3.5 meters)² = π × 12.25 square meters ≈ 38.48 square meters (rounded to two decimal places).
Example 4- Find the perimeter of a square with a side length of 9 inches.
Solution:
In a square, all sides are equal, so the perimeter is the sum of all four sides:
Perimeter = 9 inches + 9 inches + 9 inches + 9 inches = 36 inches.
1. What are 2D shapes?
- 2D shapes, or two-dimensional shapes, are geometric figures that exist in a flat plane, having only length and width dimensions. They are characterized by their outlines and have no depth or thickness.
2. What are the most common 2D shapes?
- Common 2D shapes include circles, squares, rectangles, triangles, pentagons, hexagons, octagons, and more.
3. What is the difference between 2D and 3D shapes?
- 2D shapes are flat, with only length and width dimensions, while 3D shapes have length, width, and height, giving them volume.
4. How do I calculate the area of 2D shapes?
- The formula for calculating the area of various 2D shapes, such as squares, rectangles, triangles, and circles, depends on the specific shape. For example, the area of a rectangle is length × width, while the area of a circle is πr².
5. What is the perimeter of a 2D shape?
- The perimeter of a 2D shape is the total length of its boundaries. The formula for calculating the perimeter varies based on the shape. For example, the perimeter of a square is 4 × side length.
6. Can 2D shapes have curved boundaries?
- Yes, some 2D shapes, like circles, have curved boundaries. Most other 2D shapes have straight sides or a combination of straight sides and curves.
7. What are polygons?
- Polygons are 2D shapes with straight sides and closed boundaries. Triangles, quadrilaterals (like squares and rectangles), pentagons, hexagons, and octagons are examples of polygons.
8. How are 2D shapes used in the real world?
- 2D shapes are used in various fields, including architecture, art, design, navigation, and mathematics. They play a crucial role in design, measurement, and problem-solving.
9. What is the relationship between the sides and angles in 2D shapes?
- The number of sides in a 2D shape corresponds to the number of angles. For example, a triangle has three sides and three angles, while a square has four sides and four right angles.
10. Can you give an example of a 2D shape with curved sides?
- Yes, a common example is a circle. A circle is a 2D shape with a curved boundary and no straight sides.