~In the world of geometry, the rectangle stands as a fundamental and versatile shape. It’s the basis for countless everyday objects and structures, from doors and windows to books and computer screens. In this comprehensive tutorial, we’ll delve into the world of rectangles, exploring their properties, formulas, and real-world applications.
Table of Contents:
- What Is a Rectangle?
- Properties of Rectangles
- Diagonal of a Rectangle
- Formulas for Rectangles
- Calculating Area
- Calculating Perimeter
- Real-World Applications
- Fun with Rectangles
- Rectangle Examples
Table of Contents
What Is a Rectangle?
A rectangle is a four-sided polygon (a flat, closed shape) characterized by several key features:
- Four Sides: Rectangles always have four sides.
- Opposite Sides: The opposite sides of a rectangle are equal in length.
- Right Angles: All four corners of a rectangle are right angles, meaning they form perfect 90-degree angles.

Properties of Rectangles
Rectangles have several important properties:
- Equal Opposite Sides: The two pairs of opposite sides are equal in length.
- Right Angles: All four interior angles are right angles.
- Diagonals: The diagonals (lines connecting opposite corners) are equal in length and bisect each other, dividing the rectangle into four congruent right triangles.
- Symmetry: Rectangles are symmetrical; you can fold them in half along the center to create mirror-image halves.
Diagonal of a Rectangle
The diagonal of a rectangle is a line segment that runs from one corner of the rectangle to the opposite corner. This line bisects the interior of the rectangle, creating two congruent right triangles. Here are some key characteristics of diagonals:
- Equal Length: Both diagonals of a rectangle are of equal length. They divide the rectangle into two congruent right triangles.
- Relationship with Sides: The length of a diagonal is related to the length and width of the rectangle. It can be calculated using the Pythagorean Theorem.
Diagonal of Rectangle Formula
The formula to calculate the length of the diagonal of a rectangle is based on the Pythagorean Theorem. The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the diagonal in this case) is equal to the sum of the squares of the other two sides.
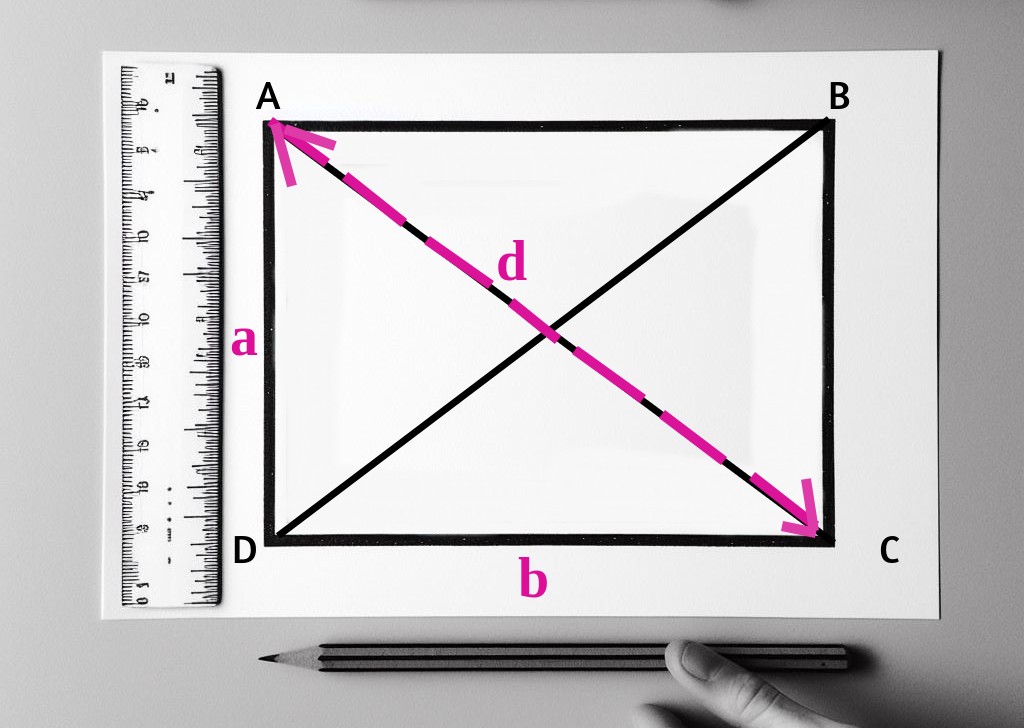
In the context of a rectangle:
- “a” represents the length of the rectangle.
- “b” represents the width of the rectangle.
- “d” represents the length of the diagonal.
The formula for the diagonal of a rectangle is:
Diagonal of Rectangle (d) = √(a² + b²)
To find the length of the diagonal, you square the length and width of the rectangle, sum the squares, and then take the square root of the result. This formula applies to all rectangles, and it helps you determine the length of the diagonal without having to measure it directly.
Formulas for Rectangles
Now, let’s explore some essential formulas for rectangles:
Area of a Rectangle
The area of a rectangle is found using the formula:
Area = Length × Width
Where:
- Length is the length of one pair of opposite sides.
- Width is the length of the other pair of opposite sides.
Perimeter of a Rectangle
The perimeter of a rectangle, which is the total length of its sides, can be calculated using the formula:
Perimeter = 2 × (Length + Width)
Real-World Applications
Rectangles are all around us, and their properties make them incredibly useful. Here are some real-world examples:
- Doors and Windows: Most doors and windows are rectangular in shape.
- Books: The pages in books are typically rectangles.
- Screens: TV and computer screens are rectangular.
- Room Layouts: Rooms are often rectangular, making them easy to design and furnish.
Fun with Rectangles
You can have fun with rectangles too! Try creating rectangular shapes in drawings, see how many rectangles you can find in everyday objects, or build a rectangular cardboard house. The possibilities are endless!
Rectangle Examples
Example 1 – Suppose you have a rectangular garden with a length of 10 meters and a width of 5 meters. Find the area of the garden.
Solution:
The formula for the area of a rectangle is:
Area = Length × Width
Substituting the given values:
Area = 10 meters × 5 meters = 50 square meters.
So, the area of the rectangular garden is 50 square meters.
Example 2 – You have a rectangular room with a length of 12 feet and a width of 8 feet. Calculate the perimeter of the room.
Solution:
The formula for the perimeter of a rectangle is:
Perimeter = 2 × (Length + Width)
Substituting the given values:
Perimeter = 2 × (12 feet + 8 feet) = 2 × 20 feet = 40 feet.
The perimeter of the rectangular room is 40 feet.
Example 3 – You’re tiling a rectangular kitchen floor that measures 6 feet in length and 4 feet in width. Each tile is 1 square foot. How many tiles do you need?
Solution:
To find the number of tiles, you need to calculate the area of the floor and then divide by the area of each tile.
Area of the floor = 6 feet × 4 feet = 24 square feet.
Area of one tile = 1 square foot.
Now, divide the area of the floor by the area of one tile:
Number of tiles = Area of the floor / Area of one tile
Number of tiles = 24 square feet / 1 square foot = 24 tiles.
You need 24 tiles to cover the rectangular kitchen floor.
FAQs
1. What is a rectangle?
- A rectangle is a four-sided polygon with four right angles and opposite sides of equal length.
2. How do you define a rectangle?
- A rectangle is defined as a quadrilateral with four right angles, where opposite sides are equal in length.
3. What are the properties of a rectangle?
- Rectangles have properties such as four right angles, equal opposite sides, diagonals that bisect each other, and symmetry.
4. What is the formula for calculating the area of a rectangle?
- The area of a rectangle is calculated by multiplying its length and width: Area = Length × Width.
5. How do you find the perimeter of a rectangle?
- The perimeter of a rectangle is determined by adding twice the length and twice the width: Perimeter = 2 × (Length + Width).
- Yes, a square is a special type of rectangle where all four sides are of equal length, making it a specific case of a rectangle.
7. What are some real-world applications of rectangles?
- Rectangles are commonly found in everyday objects such as doors, windows, books, screens, and room layouts. They are also used in architecture, design, and engineering.
8. How can I distinguish a rectangle from other shapes?
- Rectangles are distinguished by their four right angles and equal opposite sides. They have no diagonals of equal length.
9. is a Rectangle a 2d shapes
- Yes, a rectangle is a 2D shape. In geometry, 2D shapes, or two-dimensional shapes, exist in a flat plane and have only length and width dimensions.