Kites, those familiar diamond-shaped figures that grace our skies and classrooms, hold a unique place in the world of geometry. Their intriguing properties and applications extend beyond the realm of leisure. In this comprehensive article, we will explore the definition of kite, delve into their properties, and unveil their practical significance in both mathematical and real-world contexts.
Table of Contents:
- What Is a Kite Shape?
- Properties of Kite
- Diagonals of a Kite
- Area of a Kite
- Perimeter of a Kite
- Solved Examples: Applying Kite Concepts
- Kites in the Real World
- A Step-By-Step Tutorial: Navigating Kite Challenges
Table of Contents
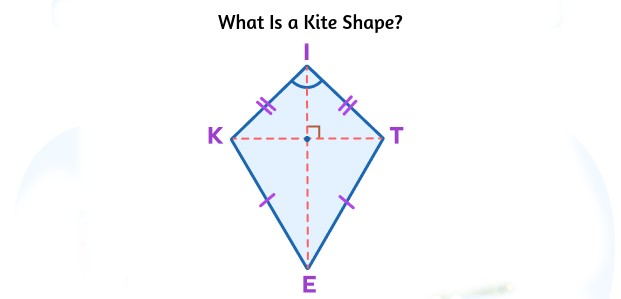
What Is a Kite Shape?
A kite is a geometric figure with the following defining characteristics:
- It is a quadrilateral, meaning it has four sides.
- Two pairs of adjacent sides are of equal length.
- One pair of diagonally opposite angles is congruent (equal).
- The diagonals intersect at a right angle.
Properties of Kite
Kites possess fascinating properties, including:
- Two Distinct Pairs of Sides: Kites have two pairs of adjacent sides, with each pair having the same length. These sides are often referred to as the “equal adjacent sides.”
- Diagonals: The diagonals of a kite are not of equal length. One diagonal is longer than the other.
- Right Angles: The diagonals intersect at a right angle, forming four right angles within the kite.
- Congruent Angles: Kites have two pairs of opposite angles, with one pair being congruent. This means they have equal measures.
Diagonals of a Kite
The diagonals of a kite have significant properties. The longer diagonal bisects the shorter diagonal, creating two congruent right triangles. Understanding these properties can simplify calculations and geometric proofs.
Area of a Kite
The area of a kite can be calculated using the following formula:
Area = 1/2 × Product of Diagonals
Where:
- “Area” represents the area of the kite.
- “Product of Diagonals” is the result of multiplying the lengths of the two diagonals that intersect within the kite.
This formula is based on the fact that the diagonals of a kite bisect each other at a right angle, creating four right triangles. By finding the area of one of these triangles and then multiplying it by 2, you can determine the total area of the kite.
Perimeter of a Kite
The perimeter of a kite can be calculated by adding the lengths of all its sides. A kite has four sides, and the perimeter formula is as follows:
Perimeter = Sum of all Side Lengths
In a kite, there are two pairs of adjacent sides with equal lengths. Let’s denote the lengths of these sides as “a” and “b” for one pair and “c” and “d” for the other pair. Therefore, the perimeter can be expressed as:
Perimeter = a+b+c+d
Simply add the lengths of the four sides to find the perimeter of the kite. Make sure to use the appropriate units, such as centimeters or inches, when working with real-world measurements.
Solved Examples
Example 1: Given a kite with diagonals of length 8 centimeters and 10 centimeters, calculate its area.
Solution:
To find the area of the kite, you can use the formula:
Area= 1/2 × Product of Diagonals
Substitute the diagonal lengths:
Area=1/2 x ×8 cm×10 cm= 80/2 sq.cm
=40 sq.cm
So, the area of the kite is 40 square centimeters.
Example 2:If a kite has two adjacent sides (a and b) with lengths of 6 inches each and the other two adjacent sides (c and d) with lengths of 8 inches each, calculate its perimeter.
Solution:
To calculate the perimeter of the kite, add the lengths of all its sides:
Perimeter= a+b+c+d
Substitute the side lengths:
Perimeter= 6 inches + 6 inches + 8 inches + 8 inches = 28 inches
So, the perimeter of the kite is 28 inches.
FAQs
1. What is a kite in geometry?
A kite in geometry is a four-sided geometric shape with two pairs of adjacent sides of equal length. It also has diagonals that intersect at a right angle.
2. What are the key properties of a kite?
Key properties of kites include having two pairs of equal adjacent sides, diagonals that are not of equal length, and diagonals that intersect at a right angle. Kites also have two pairs of opposite angles, with one pair being congruent.
3. How do you calculate the area of a kite?
To calculate the area of a kite, you can use the formula: Area = 1/2 × Product of Diagonals. Multiply the lengths of the two diagonals and divide the result by 2.
4. What is the perimeter of a kite?
The perimeter of a kite is found by adding the lengths of all its sides. This includes the sum of the lengths of the two pairs of adjacent sides.
5. Are kites used in real-world applications?
Yes, kites have practical applications in fields such as architecture, engineering, and design. They can be found in structures, sail design, and other areas where their unique properties are useful.
6. What’s the relationship between the diagonals of a kite?
The longer diagonal of a kite bisects the shorter diagonal, creating two congruent right triangles. This relationship is useful for various geometric calculations.
7. Can a rectangle be considered a kite?
No, a rectangle is not considered a kite. While a rectangle has four right angles, it does not have the unique side length and diagonal relationships that define a kite.